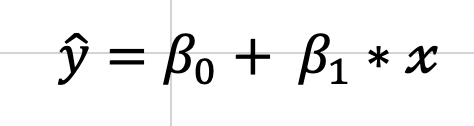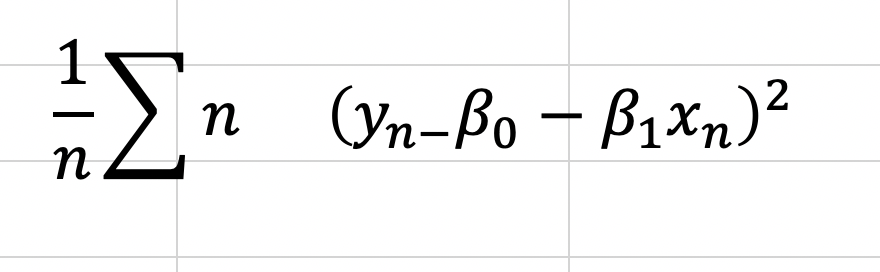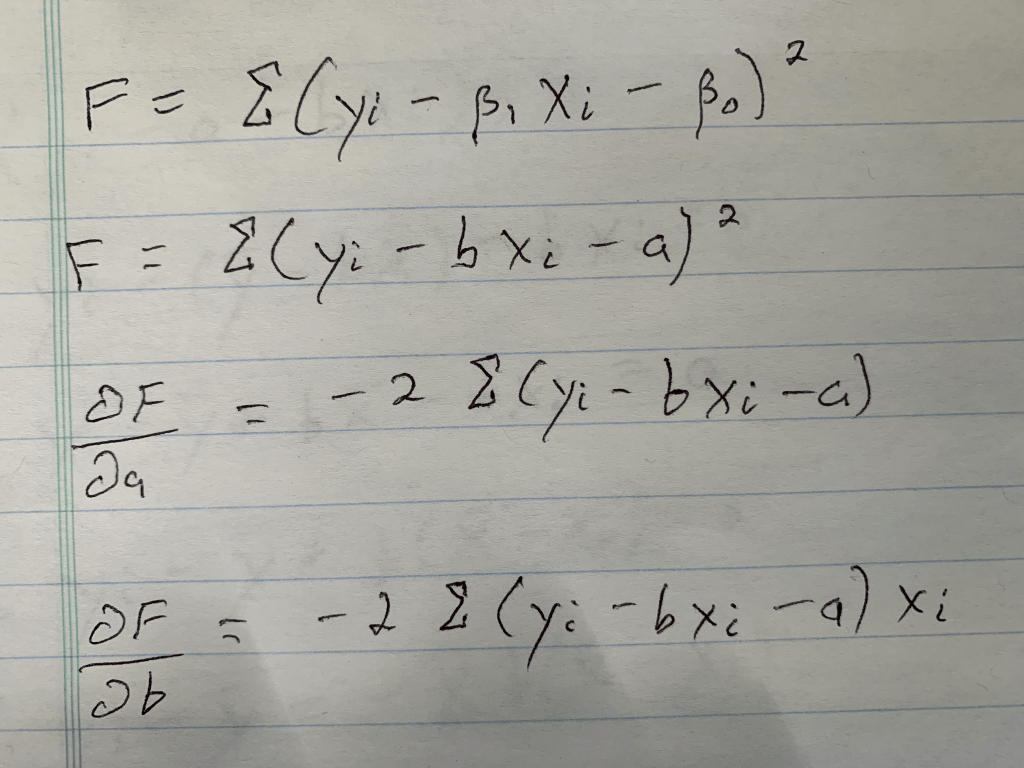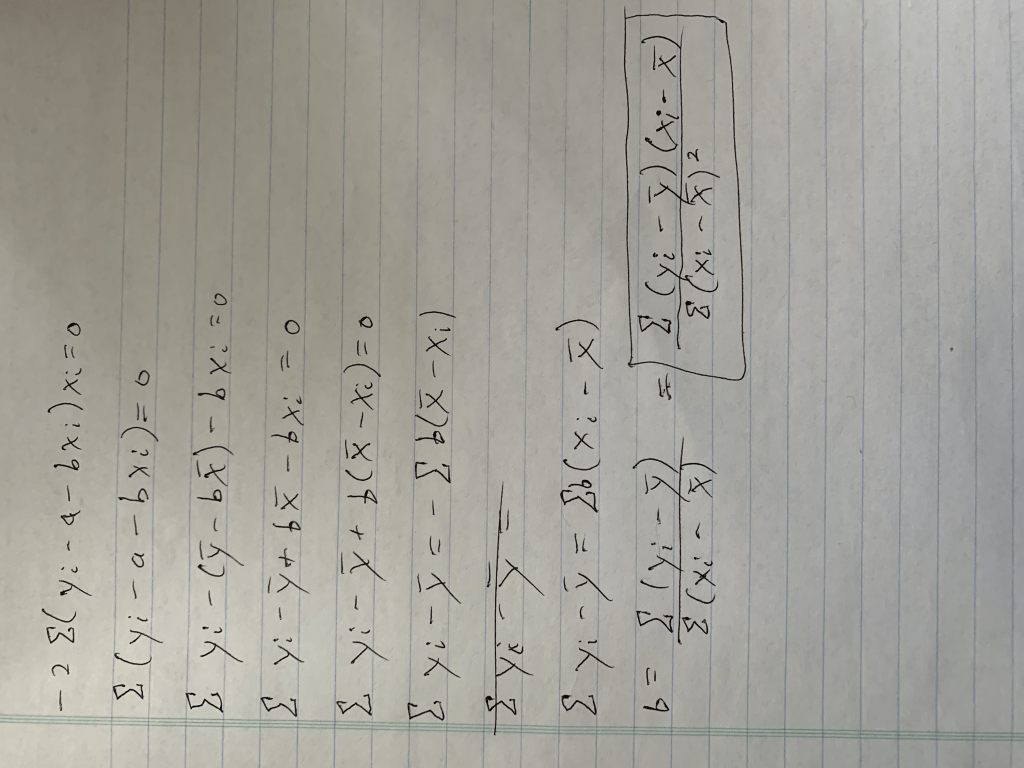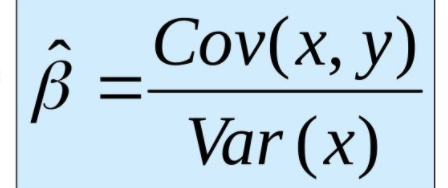Machine Learning | Inquiries

Pokemon: EDA and Battle Modeling

Posted on March 8, 2021 by josephcohen94

Exploratory data analysis and models for determining which Pokemon tend to have the biggest pure advantages in battle given no items in play.

Thanks for visiting my blog today!

Context

Pokémon is currently celebrating 25 years in the year 2021 and I think this is the perfect time to reflect on Pokémon from a statistical perspective.

Introduction

If you’re around my age (or younger), then I hope you’re familiar with Pokémon. It’s the quintessential Gameboy game we all used to play as kids before we started playing “grown-up” games on more advanced consoles. I remember how excited I used to get when new games would be released and I remember equally as well how dejected I was when I lost my copy of the Pokémon game “FireRed.” Pokémon has followed a basic formula running through each iteration of the game, and it’s pretty simple. It revolves around creatures known as “Pokémon.” You start with a “starter” Pokémon who usually has high potential but starts with very little power and you then can catch Pokémon, train Pokémon, buy items, beat gym leaders, find “legendary” Pokémon (I suppose the word “Pokémon” works as singular and plural), create a secret base, trade Pokémon with other gameboy owners, and of course – beat the Elite 4 like 500 times with different parties of Pokémon. With each new set of games (games were released in sets usually labeled by a color – silver & gold and green & red – as two examples), came a new group of Pokémon. The first generation was pretty bland. There were some cool ones like Charizard, Alakazam, and Gyarados but there were far more weird and boring ones like Slowpoke (Slowpoke has got to be the laziest name ever), Pidgey (second most lazy name?), and Arbok (Cobra backwards, yes it’s a snake). As the generations of Pokémon new to each set of games progressed there was a lot more diversity and creativity. Some generations like Gen 2 and Gen 3 really stuck out in my head. Examples include Skarmory and a special red (not blue) Gyarados in Gen 2 and Blaziken and Mightyena in Gen 3. The most important part of the Pokémon games are battles. Pokémon grow in skill and sometimes even transform in appearance through battling and gaining experience. You also earn badges and win prize money through battles. Battles are thrilling and require planning and tactics. This is expressed in many ways; the order of your Pokémon in your party, the type of Pokémon you bring to counteract your potential opposing Pokémon, the items you use to aid you in battle, when you choose to use certain moves (there is a limit to the amount of times each move can be used), switching Pokémon in battle, sacrificing Pokémon, diminishing the health of a “wild” Pokémon to the point where it doesn’t faint but is weak enough to be caught, and there’s a lot more I could probably add. Ok, so the point of this blog is to look for interesting trends and findings through visualizations in the exploratory data analysis section (EDA) and later I will examine the battles aspect and look for key statistics that indicate when a Pokémon is likely to win or lose a battle.

Let’s get started!

Data

My data comes from Kaggle and spans about 800 Pokémon across the first 6 generations of the series. I’d like to quickly note that this includes mega-Pokémon which are basically just more powerful versions of certain regular Pokémon. Let me show you what I mean; we have Charizard at the top of this post and below we have mega-Charizard.

3D Printed Mega Charizard X - Pokemon by Gnarly 3D Kustoms | Pinshape

Yeah, it’s pretty cool. Anyway, we also have legendary Pokémon in this dataset but, while legendary Pokémon may have mega types, they are not a fancy copy of another Pokémon. I’ll get more into how I filtered out mega Pokémon in the data prep section. One last note on Pokémon classes – there are no “shiny” Pokémon in this data set. Shiny Pokémon are usually not more powerful than their regular versions but they are more valuable in the lexicon of rare Pokémon. Next, we have 2 index features (why not just 1?). Pokémon are by construction at least one “type.” Type usually connects to an element of nature. Types include grass, poison, and fire (among others) but also less explicit and nature-related terms such as dragon, fairy, and psychic. A Pokémon can have up to two types with one usually being primary and the other secondary. Type is a critical part of battles as certain types have inherent advantages and disadvantages against other types (fire beats grass but water beats fire, for example). Unfortunately, creating a dataset containing battle data between every possible Pokémon would be a mess and we therefore are going to use the modeling section to see what types of Pokémon are strongest in general, and not situationally. Our next features will be related to Pokémon stats. HP – or hit points – represent your health. After Pokémon get struck with enough attack power (usually after a couple turns), their HP runs out and they faint. This takes me to the next four features: attack, defense, special attack, and special defense. Attack and defense are the baseline for a Pokémon’s, well… attack and defense. Certain moves may nullify these stats though. A great example is a one-hit knockout move; attack doesn’t matter at all. Special attack and special defense are the same as attack and defense but refer to moves where there is no contact between Pokémon. So a move like “body slam” is attack-based while a move like “flamethrower” is special attack based. Total represents the sum of HP, special attack/defense, attack/defense and speed. Speed is a metric that basically determines who strikes first in battle. Occasionally some moves will take precedence and strike first but in the absence of those moves the turn-based battle begins with the attack of the faster Pokémon. The feature generation refers to which generation between 1 and 6 that the Pokémon in question first appeared in. Pokémon often make appearances in later generations once introduced in a previous generation. This is sometimes the case for legendary Pokémon as well. This takes us to our next feature which is a binary legendary Pokémon indicator. Legendaries are Pokémon that appear once per game usually in one specific spot that are generally quite powerful (and cool-looking). There are “roaming legendaries” that are unique but will appear at random locations until caught as opposed to being confined to one special location. Most legendaries are delegated to specific areas at specific points in a game’s storyline. Latios and Latias, from Pokémon Ruby and Sapphire are roaming and are incredibly hard to locate and subsequently catch while Groudon and Kyogre are easier to find and catch and play a key role in the storyline of their respective games. Finally, our last feature is win rate (and it’s continuous) – and that is the target feature. I added some features to the dataset which will be discussed below. The only one I’ll mention now is that I binned win rate into three groups in order to have a discrete model as well.

Data Preparation

This section will outline how I manipulated my data for modeling purposes. I started by dropping extra columns like the index feature. Next, I created a feature which was a binary representation of whether a Pokémon was of one or two types. I also scanned the data to see if the word “mega” appears in any names and added a feature to indicate if a Pokémon was or was not a mega type. In addition to the collective data I also separated datasets into common, mega, and legendary Pokémon while aiming for no overlapping Pokémon. I had enough data where I could comfortably delete all rows with null values. I added another feature as well to measure the ratio of special attack divided by attack and did the same with defense. I originally thought special attack meant something different than what it actually means and ended up calling these features “attack bonus” and “defense bonus.” Next, I filtered out any rows containing numerical outliers which would be 2.5 standard deviations away from the rest of the data in said feature. This reduced my data by about 15%. Next, I applied max-absolute scaling to gauge the value of each data point relative to the other values in each feature (this puts every result somewhere between 0 for low and 1 for high). I also noticed through hypothesis tests that speed might have an outsized impact on battle outcome (more on this later) so created an extra feature called “speed ratio” to reflect how much of a Pokémon’s total comes from speed alone. To deal with categorical data, I leveraged target encoding. I published an article on Towards Data Science which can be found here if you would like to learn more about target encoding. This was the end of my main data prep. I did a quick train-test-split which pertains more to modeling but is technically an element of data prep.

EDA

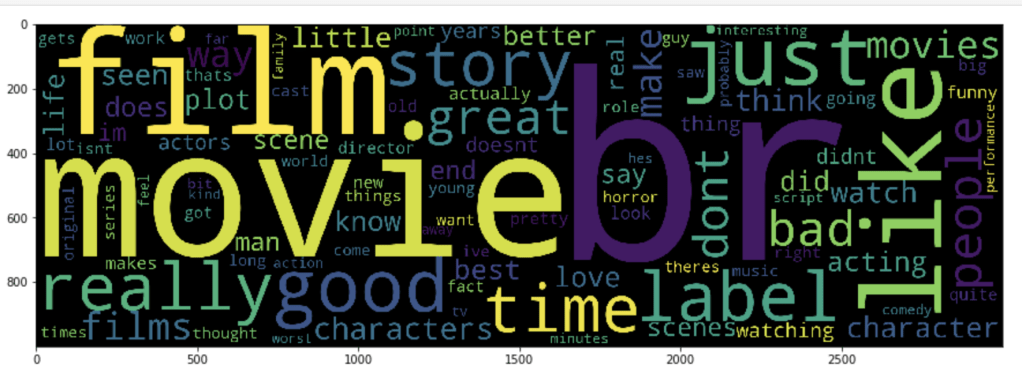
This section contains a sampling of all the exciting graphs to describe what Pokémon has looked like over the years.

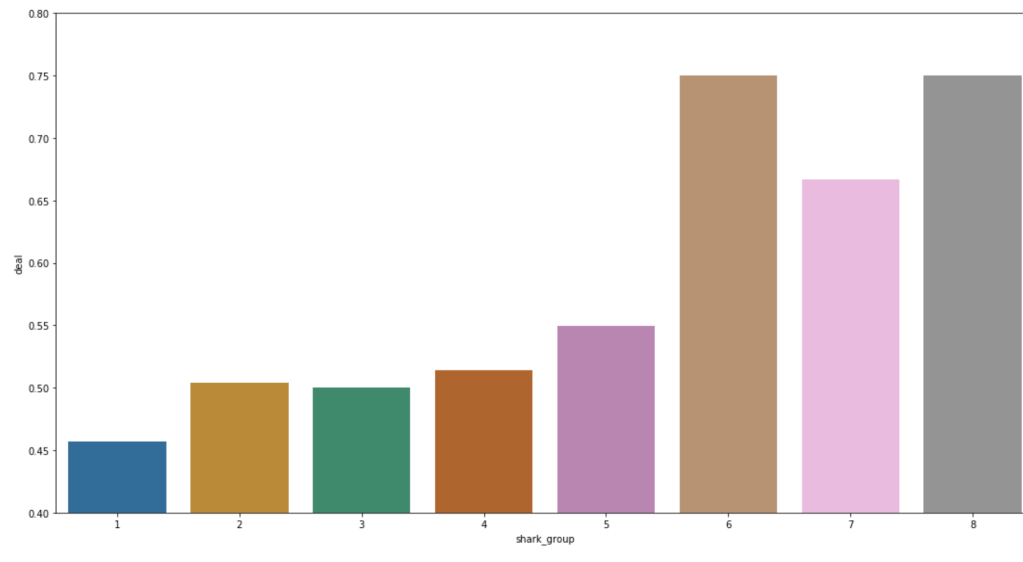
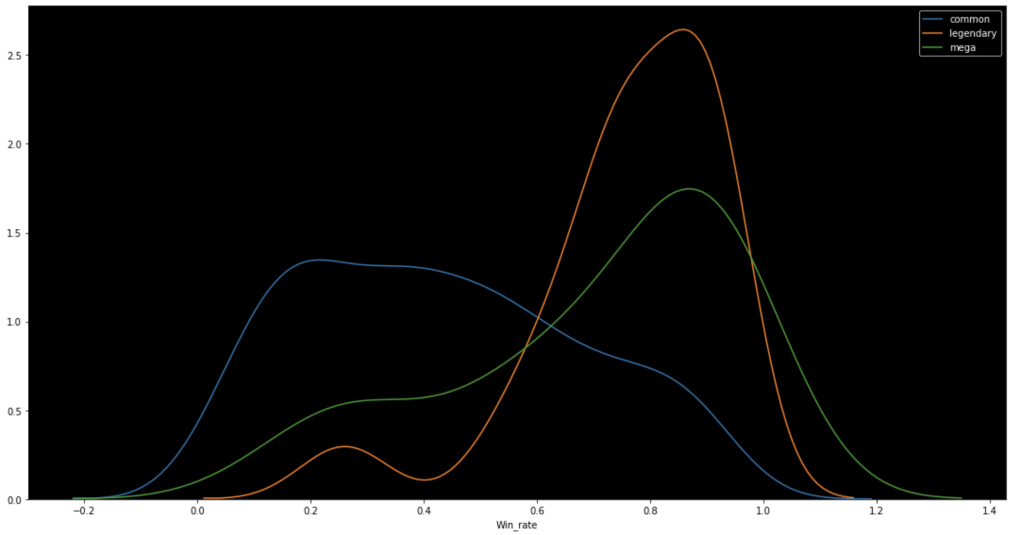
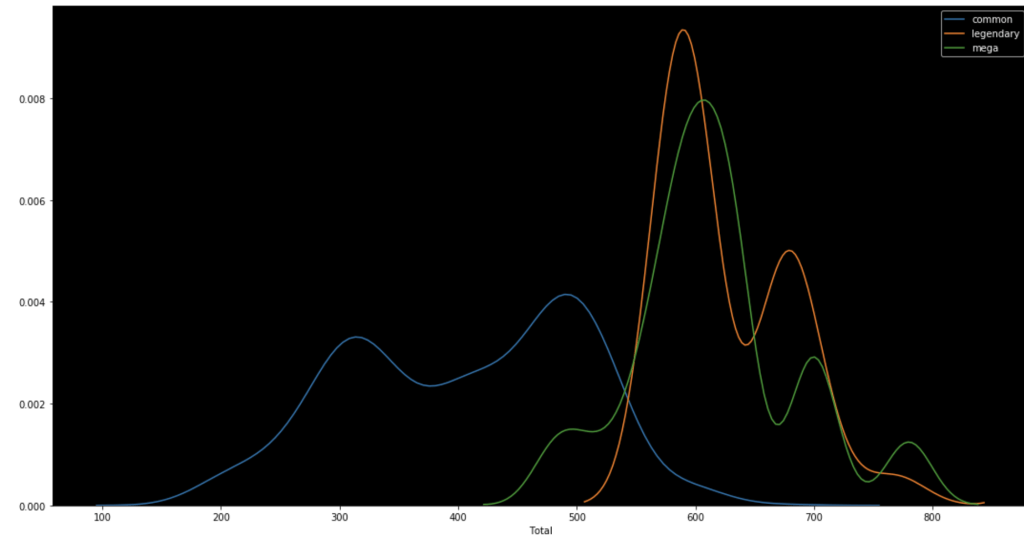
The following graph shows the distributions of win rate and total stats respectively segmented by Pokémon class.

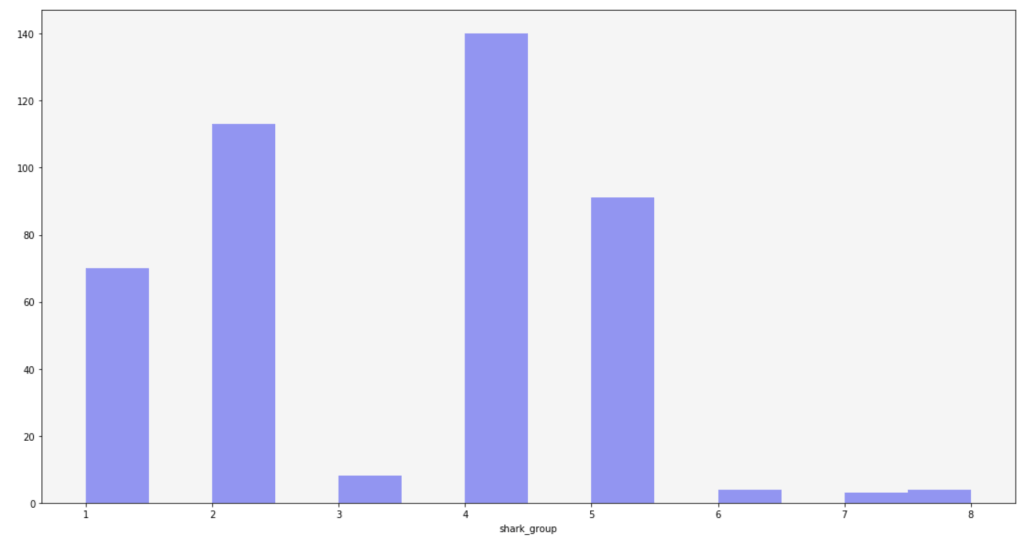
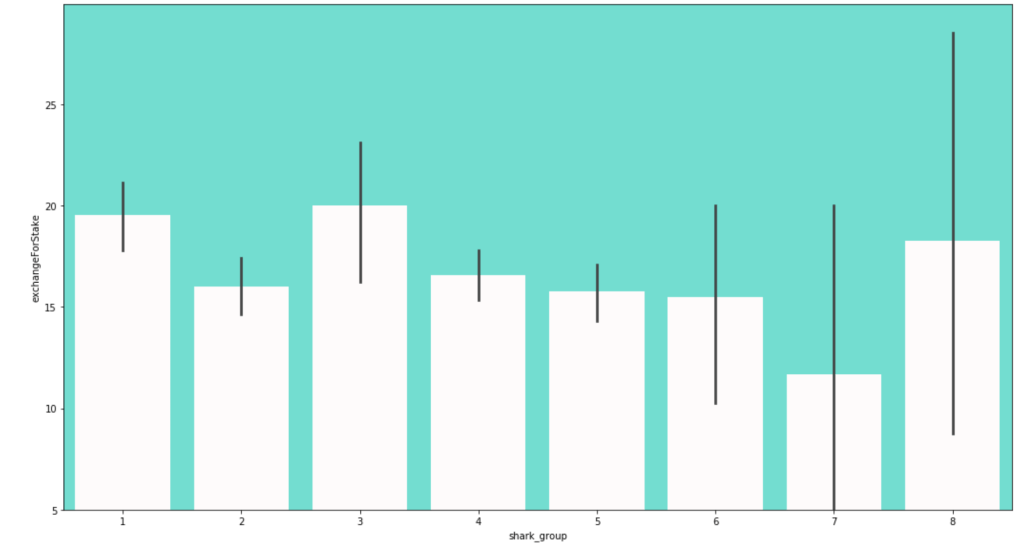
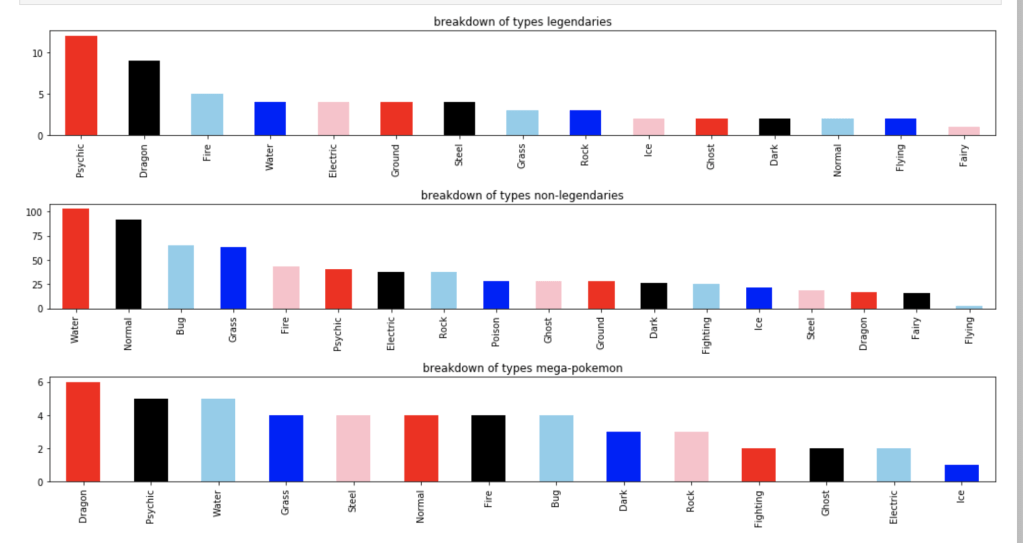
The following graph shows how many Pokémon appear for each type:

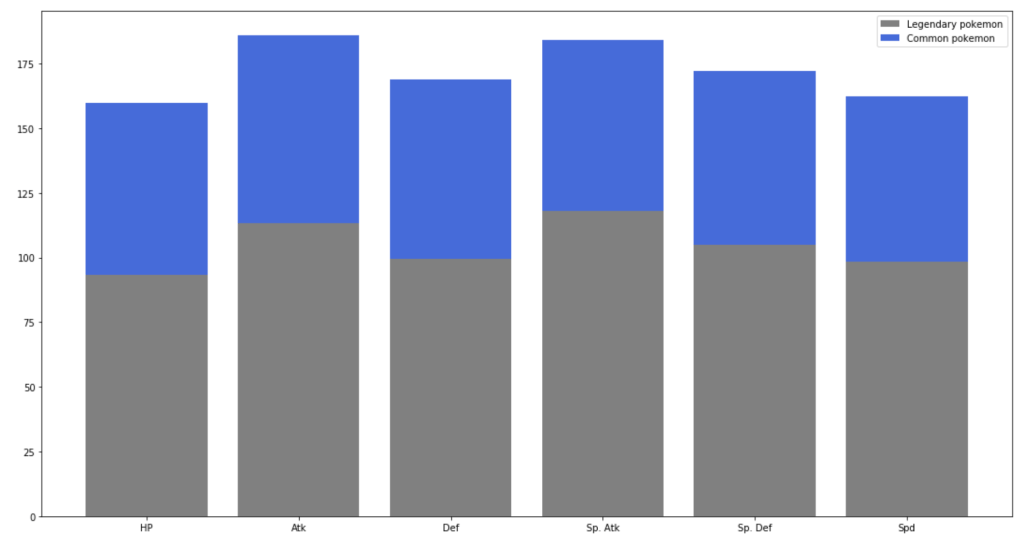
The graph below shows the difference between stats of legendary Pokémon and regular ones.

And next…

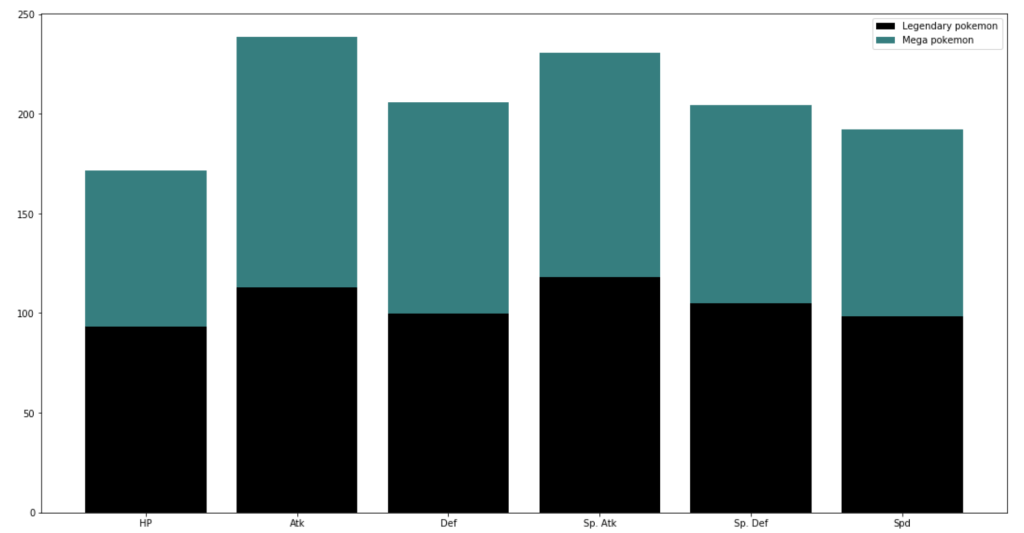
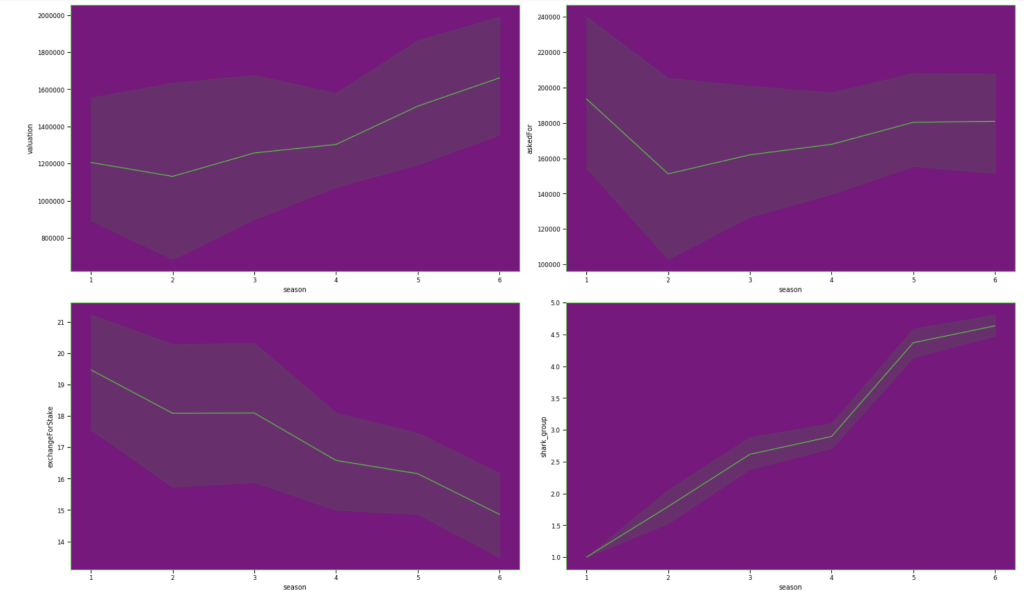
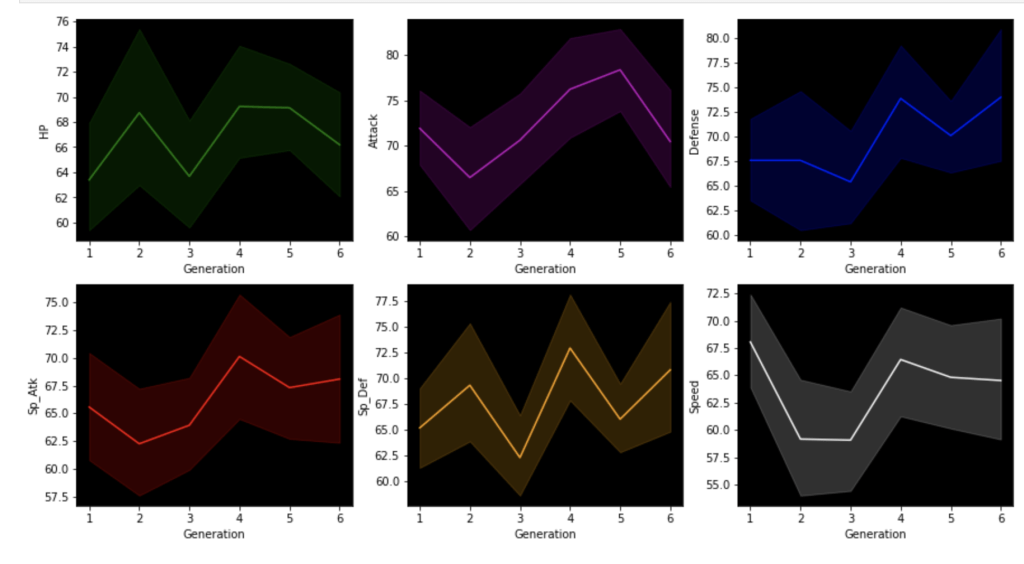
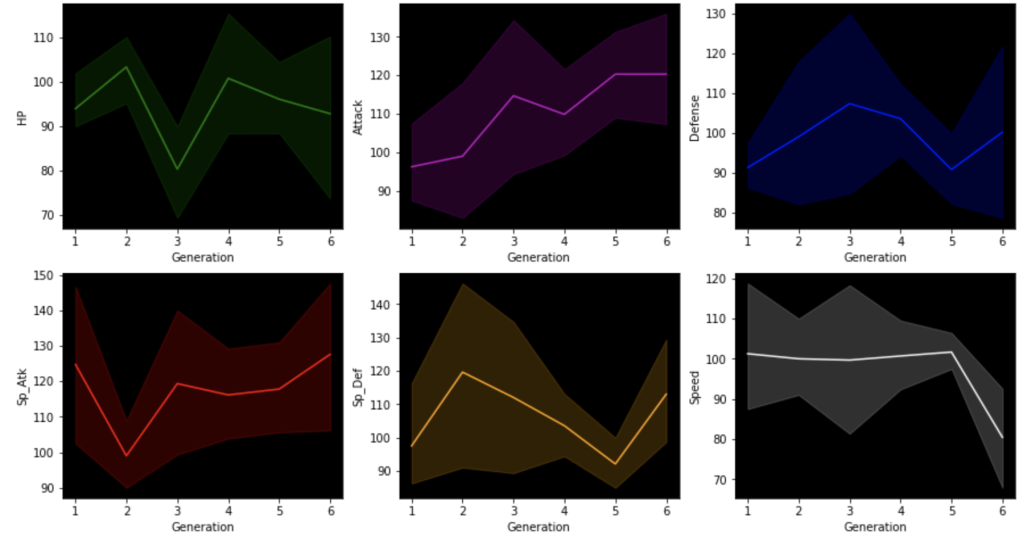
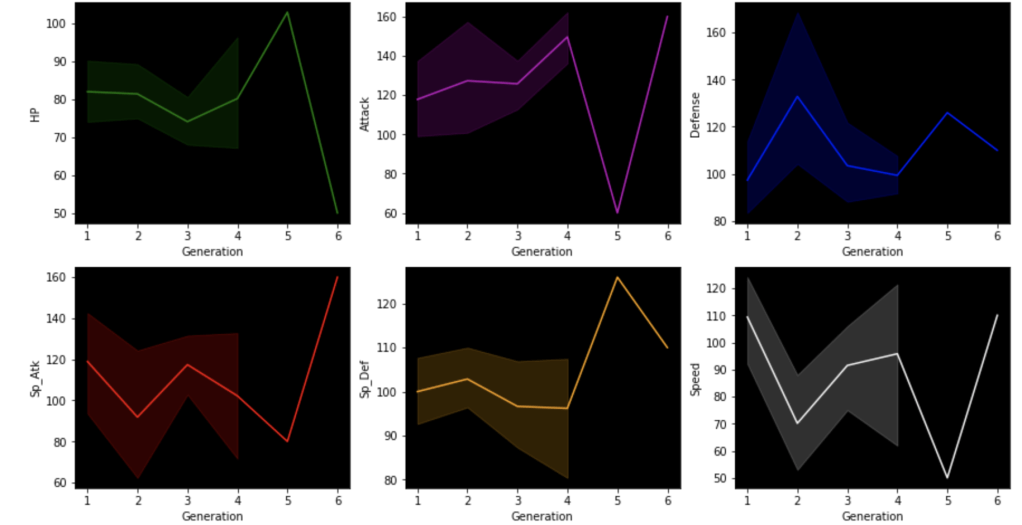
This next set of visuals show trends over the years in common, legendary, and mega Pokémon respectively.

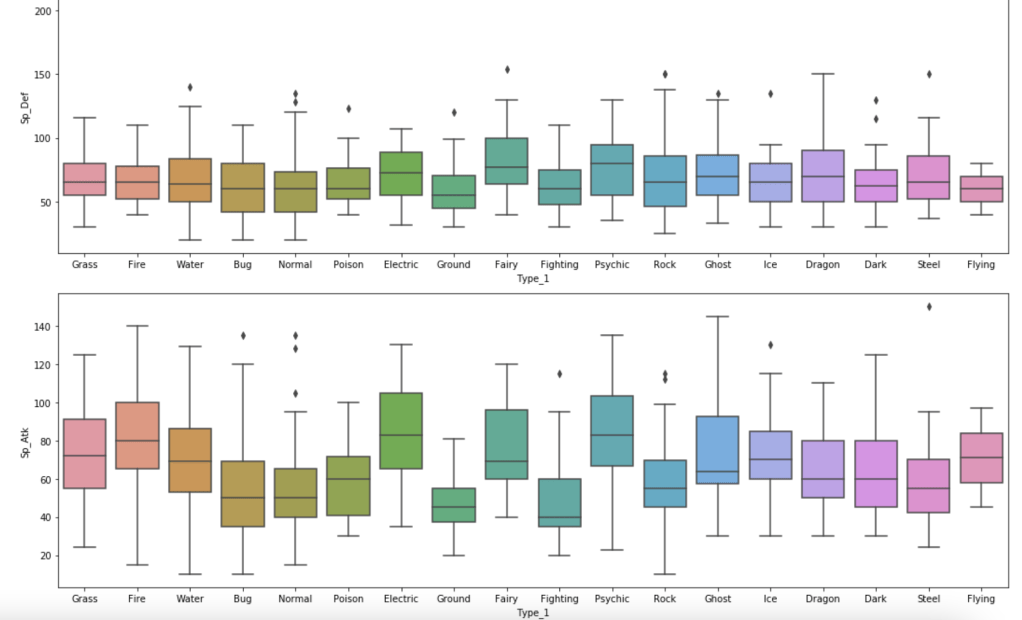
The next series of charts shows the distribution of stats by type with common Pokémon:

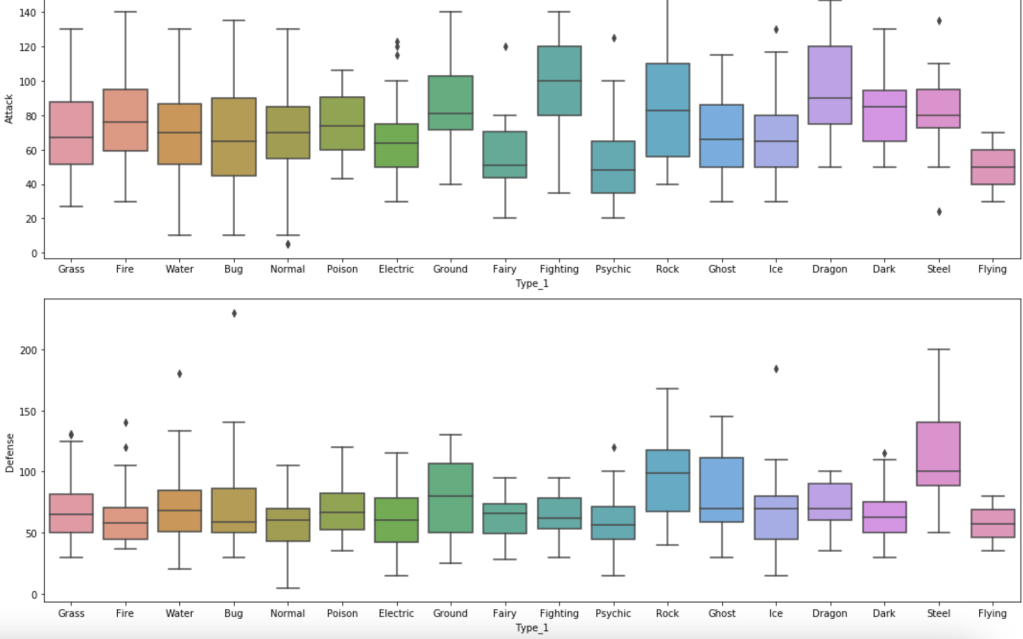
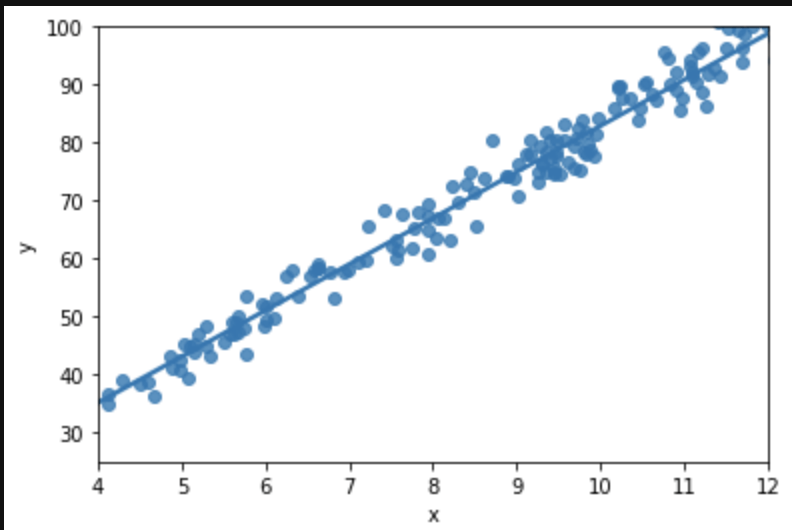
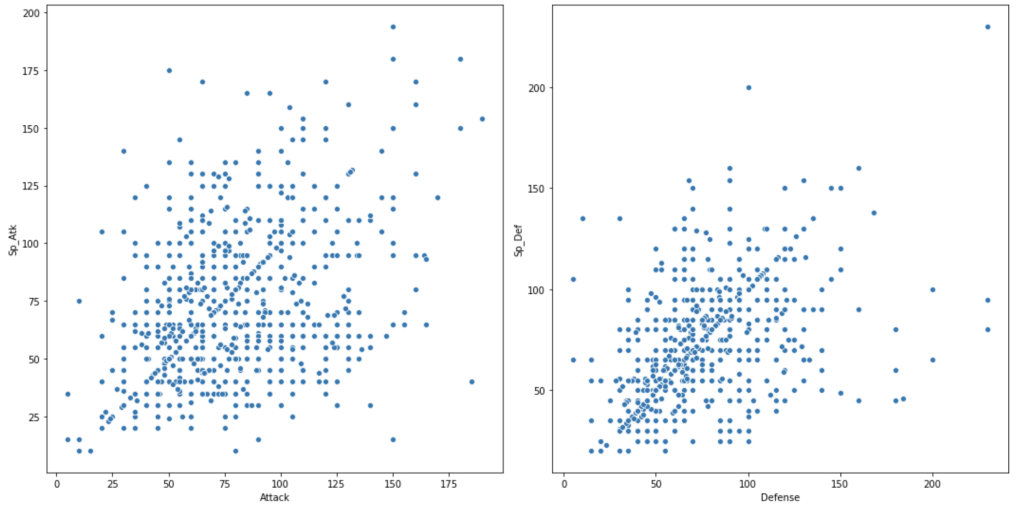
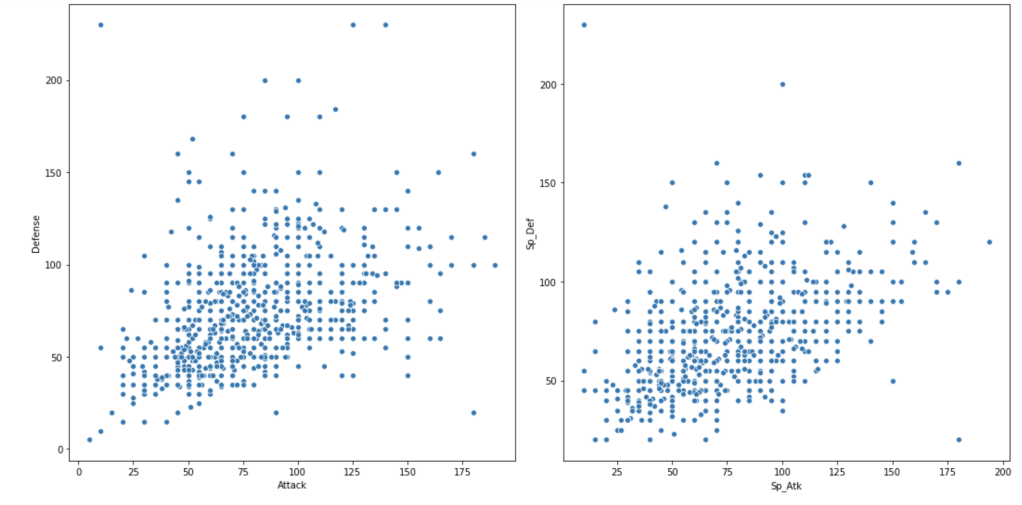
Next, we have scatter plots to compare attack and defense.

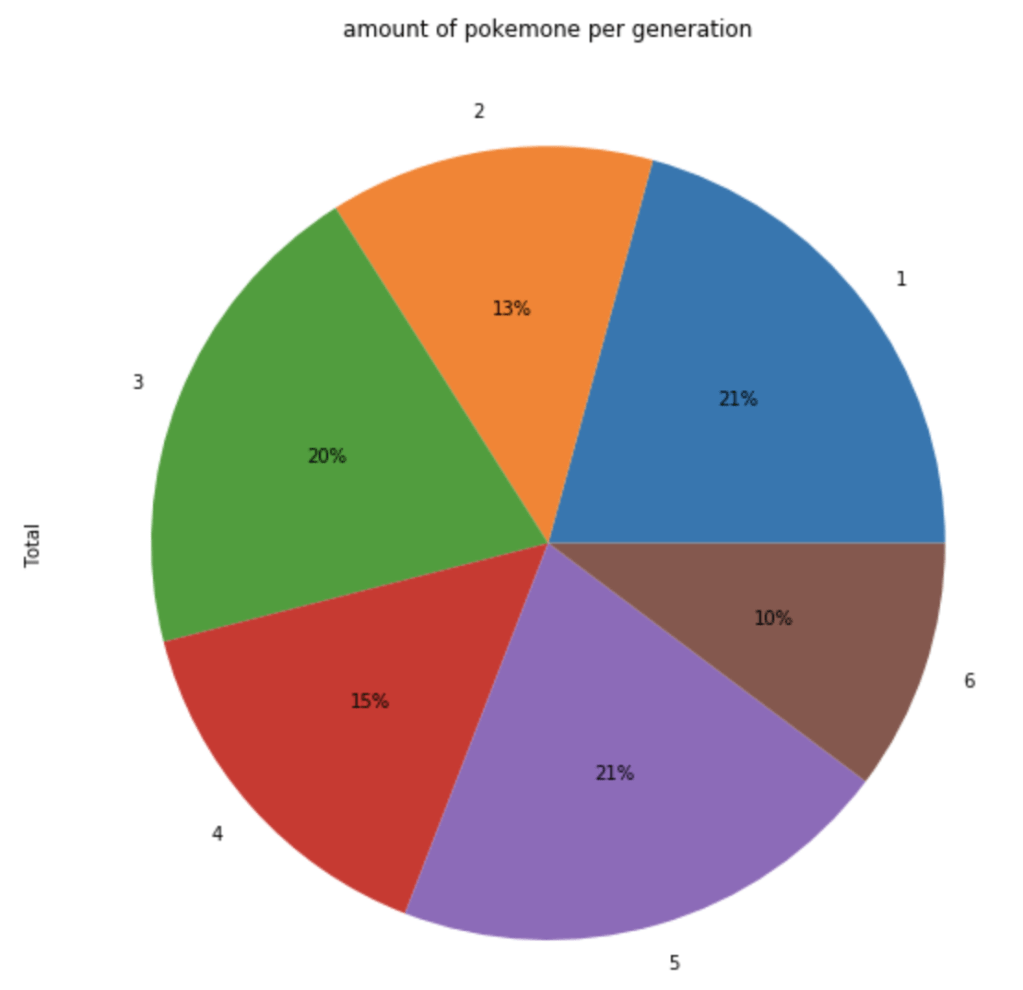
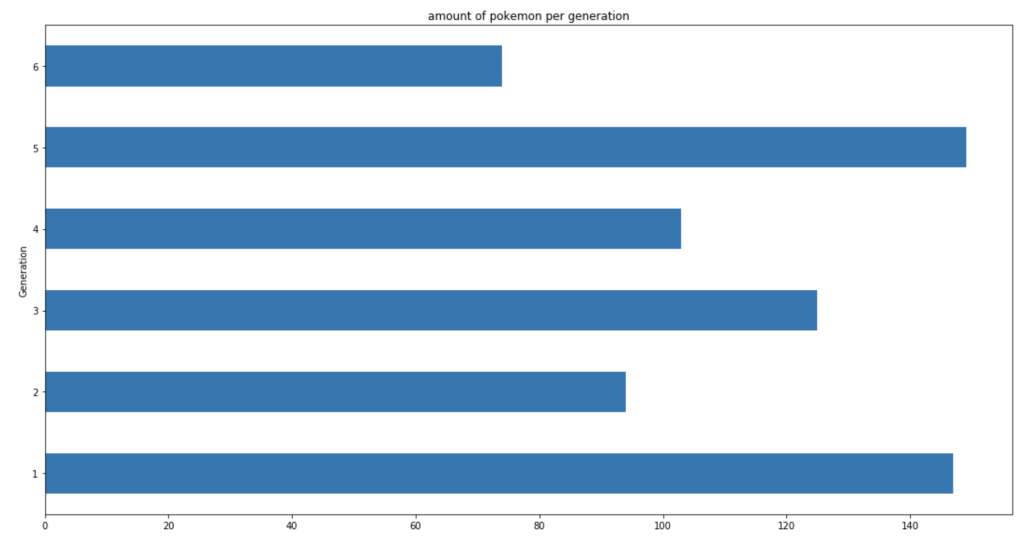
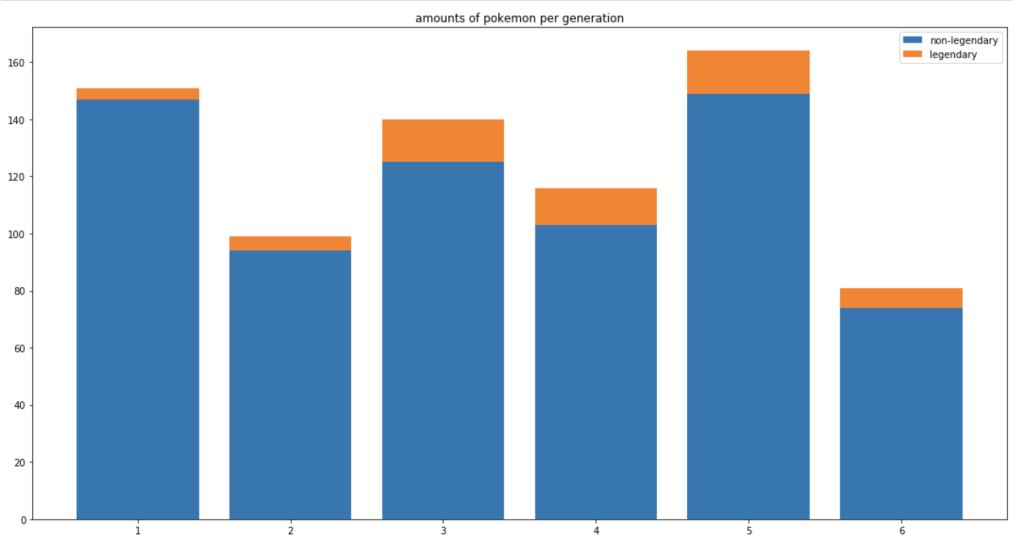
The next chart shows the distribution of total Pokémon across 6 generations.

Let’s look at legendary and mega Pokémon.

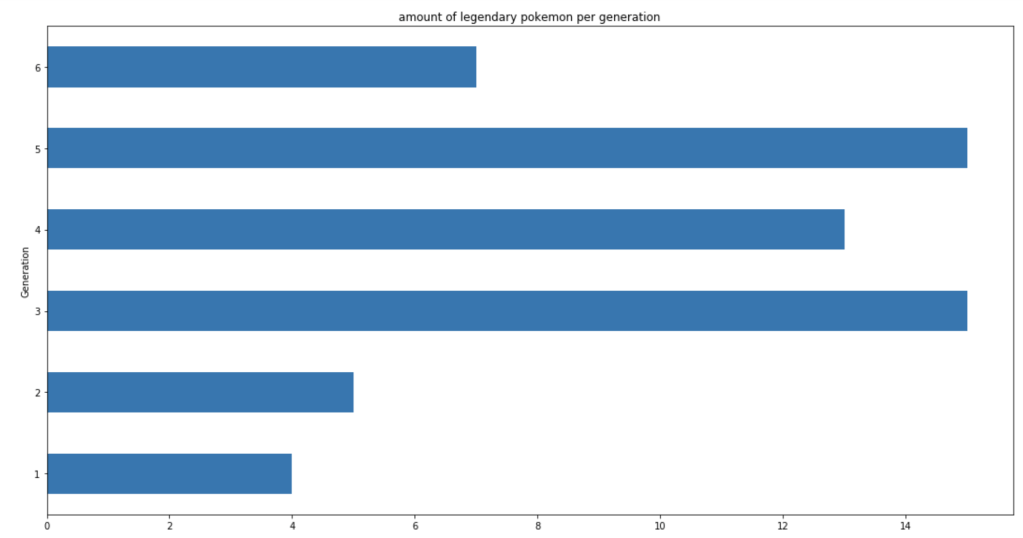
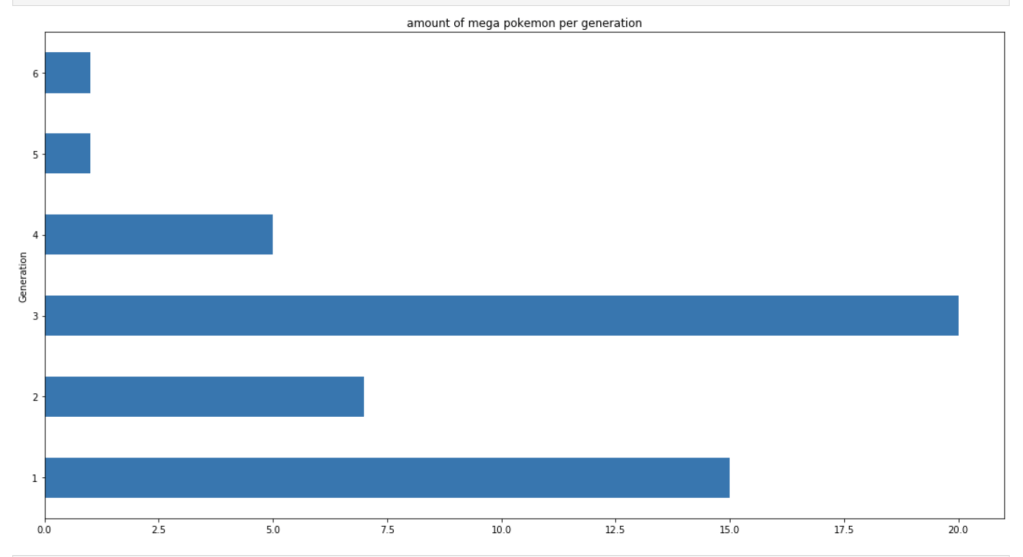
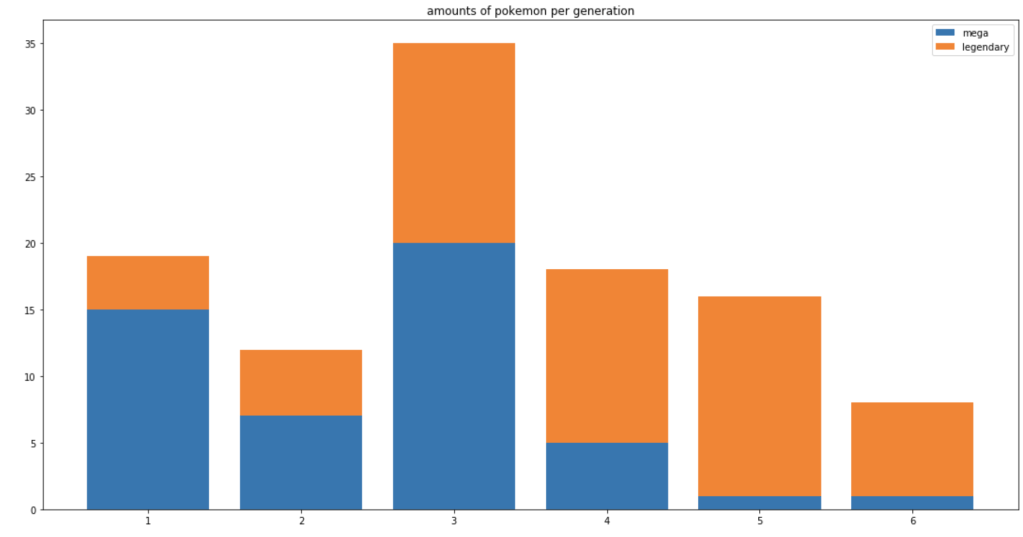
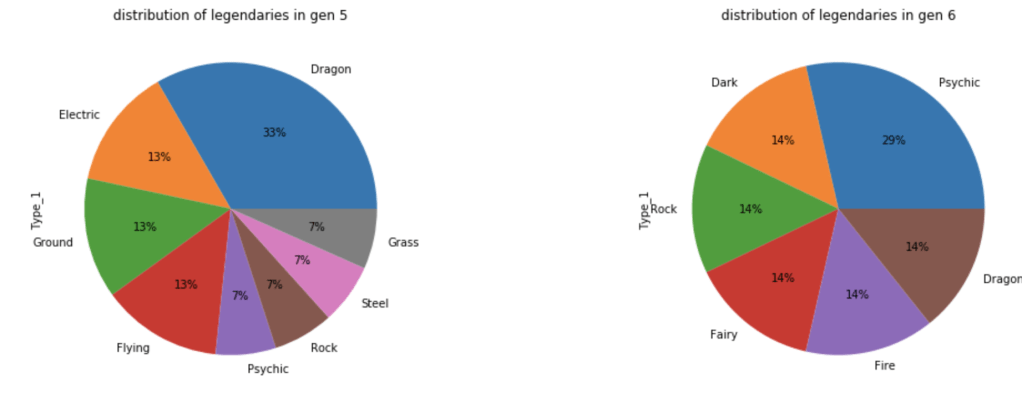
Let’s look at how these legendaries are distributed by type.

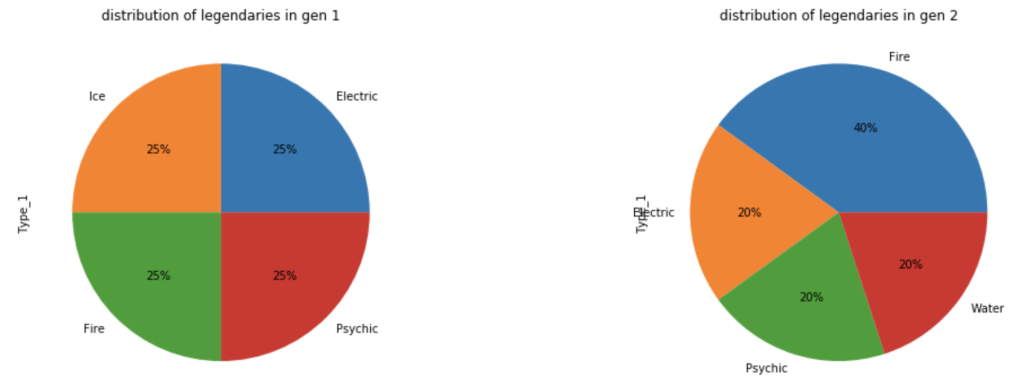
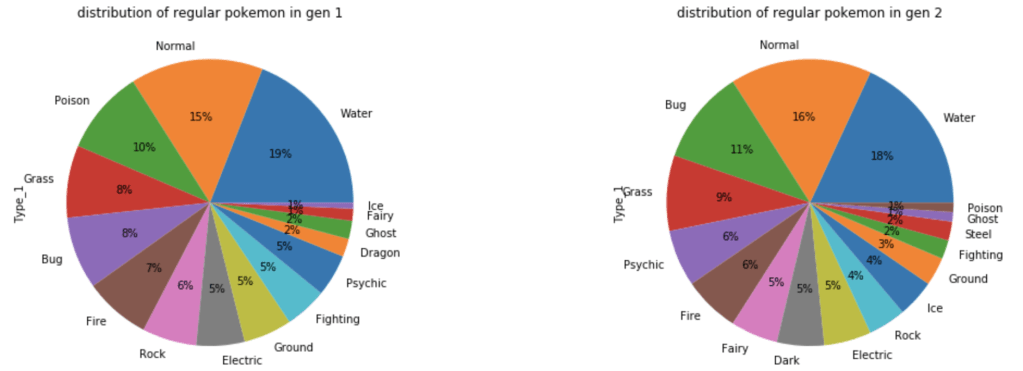
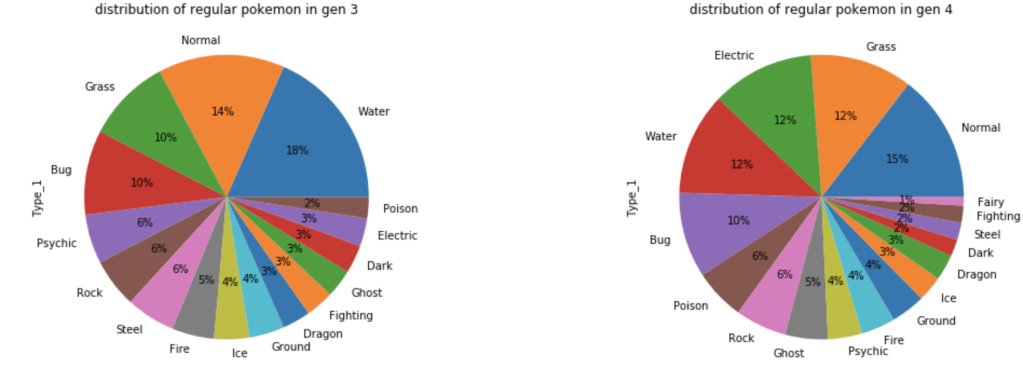
What about common Pokémon?

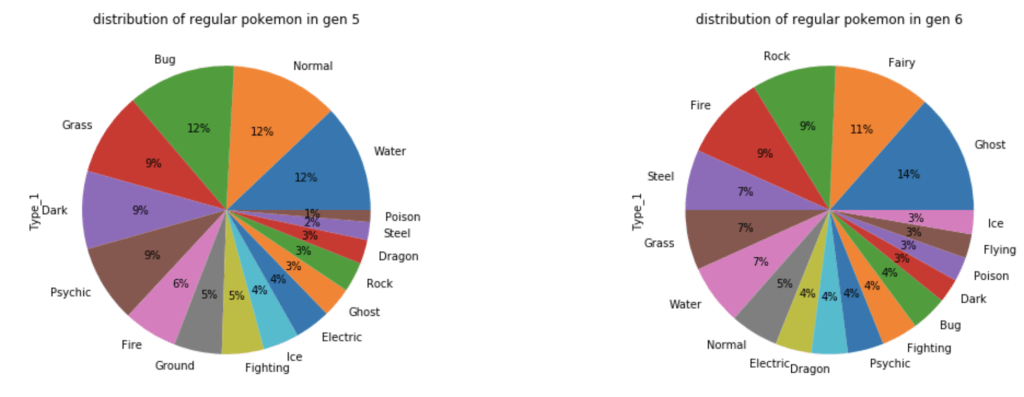
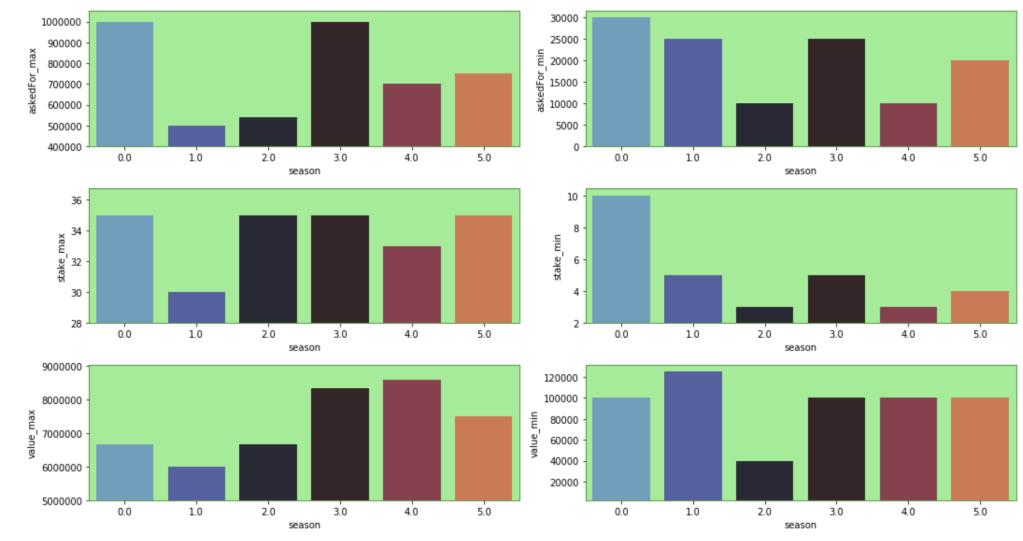
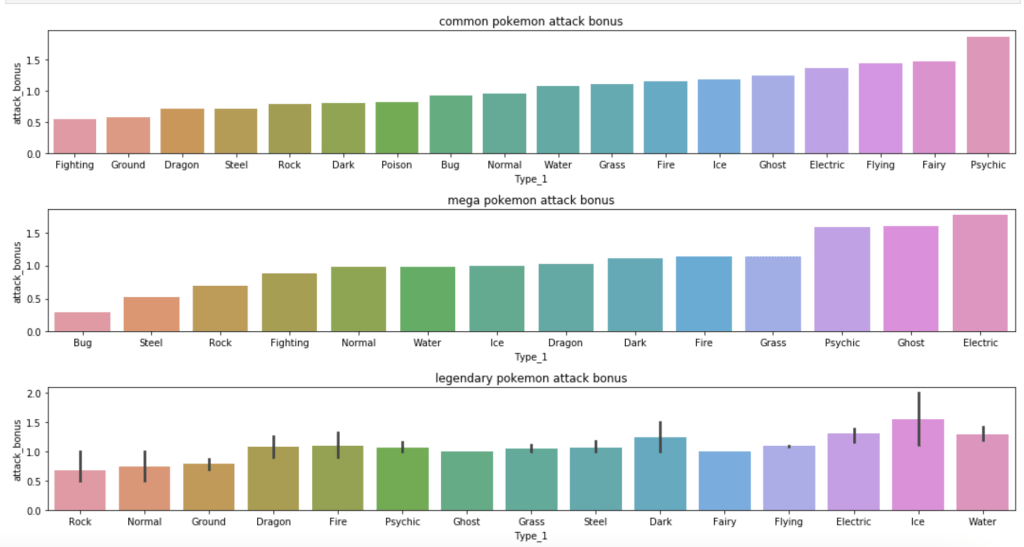
The next group of visuals shows distribution of stats by generation among legendary Pokémon.

The next set of visuals shows which Pokémon have the highest ratio of special attack to attack

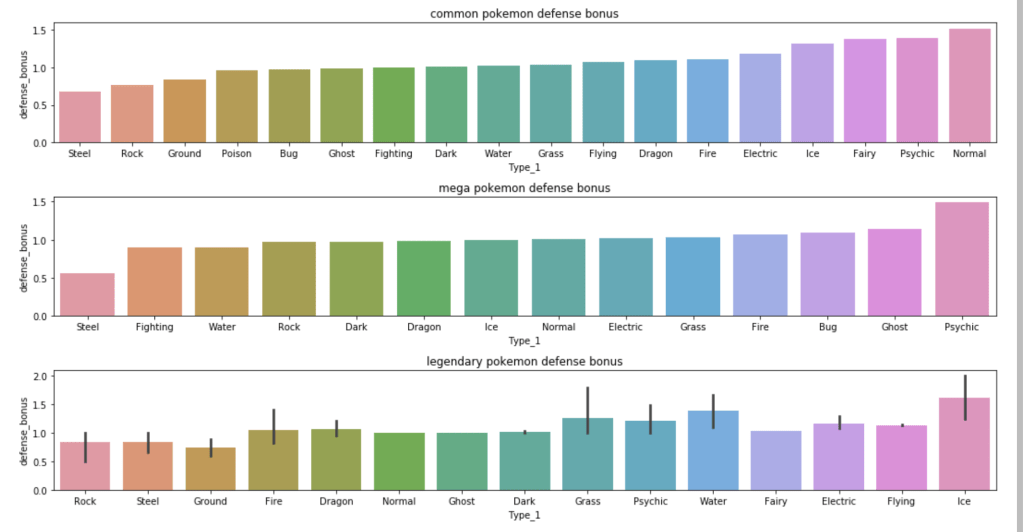
The next set of visuals shows which Pokémon have the highest ratio of special defense to defense

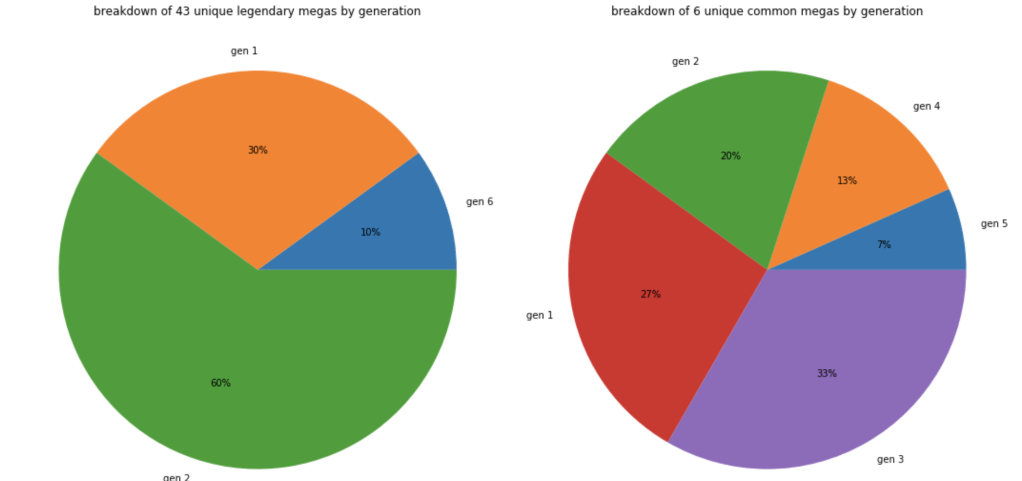
This next set of charts show where mega Pokémon come from.

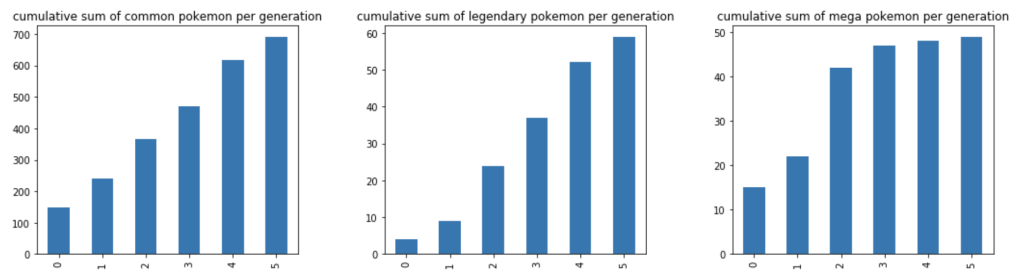
Next, we have a cumulative rise in total Pokémon over the generations.

Models

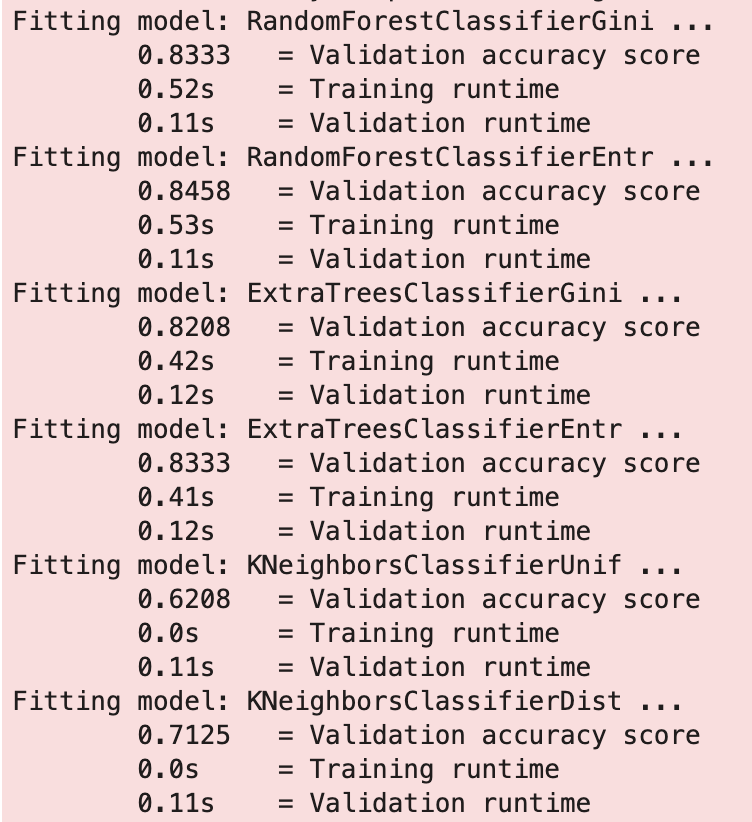
As I mentioned above, I ran continuous models and discrete models. I ran models for 3 classes of Pokémon: common, legendary, and mega. I also tried various groupings of input features to find the best model while not having any single model dominated by one feature completely. We’ll soon see that some features have outsized impacts.

Continuous Models

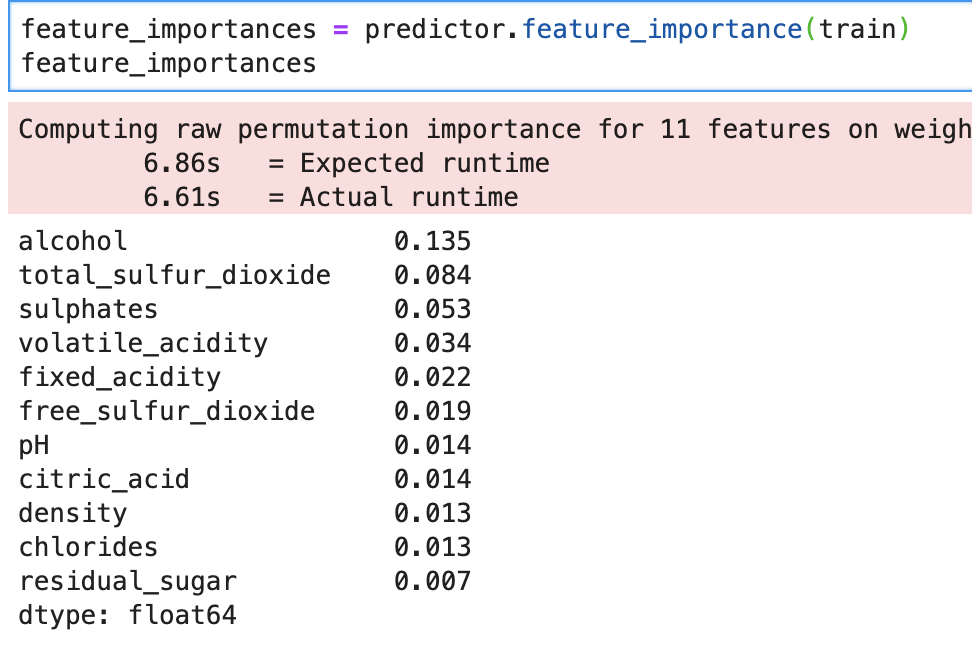
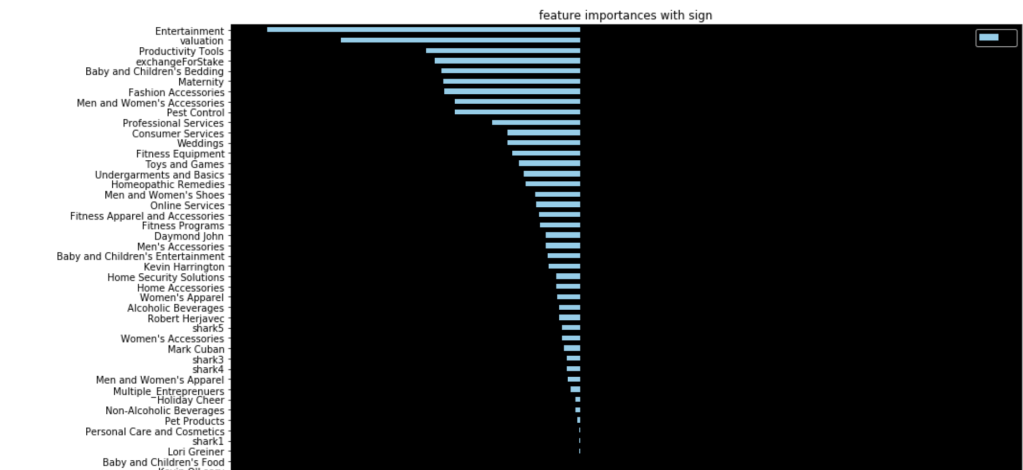
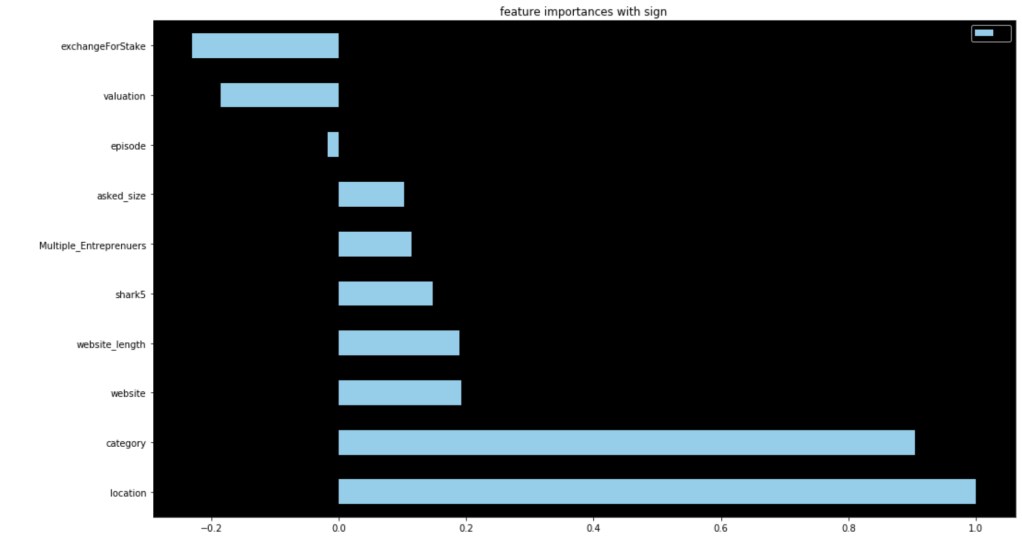
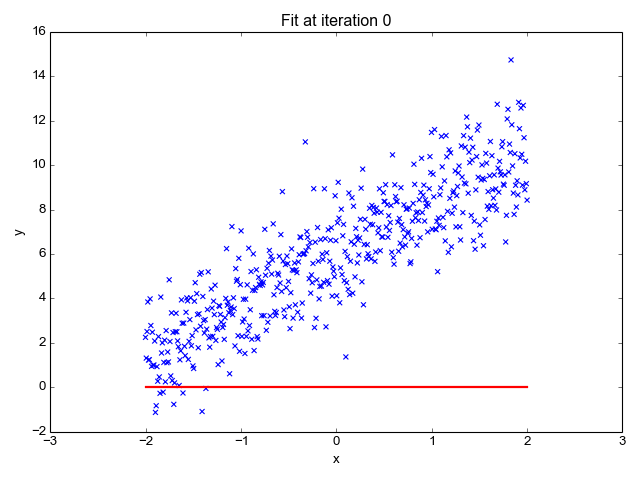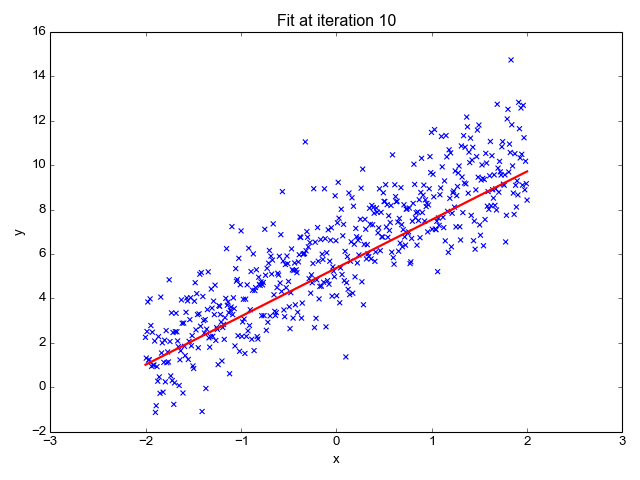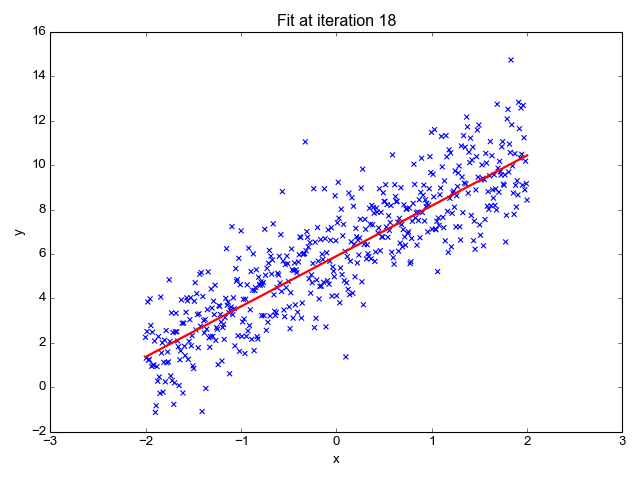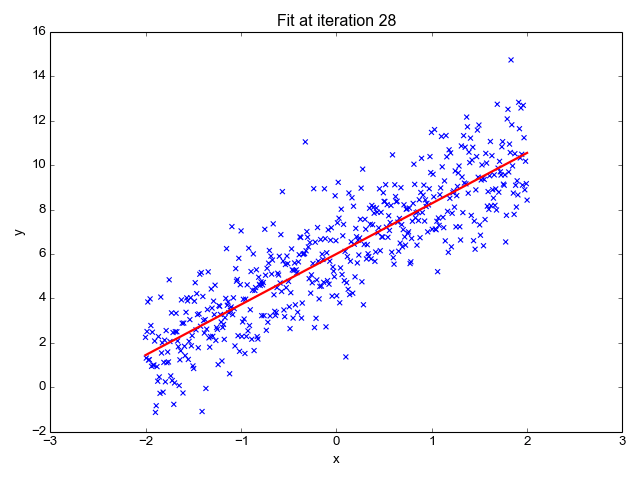
The first and most basic model yielded the following feature importance while having 90% accuracy:

Speed and speed ratio were too powerful, so after removing them my accuracy dropped 26% (you read that right). This means I need speed or speed ratio. I chose to keep speed ratio. Also, I removed the type 1, type 2, generation, and “two-type” features based on p-values. Now, I had 77% accuracy with the following feature ranks.

I’ll skip some steps here, but the following feature importances, along with 75% accuracy, seemed most satisfactory:

Interestingly, having special attack/defense being higher than regular attack/defense is not good. I suppose you want a Pokémon’s special stats to be in line with regular ones.

I’ll skip some steps again, but here are my results for mega and legendaries within the continuous model:

Legendary with 60% accuracy:

Mega with 91% accuracy:

Discrete Models

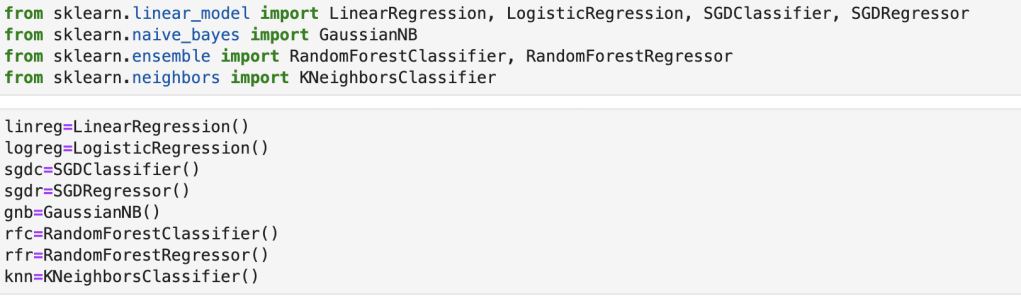
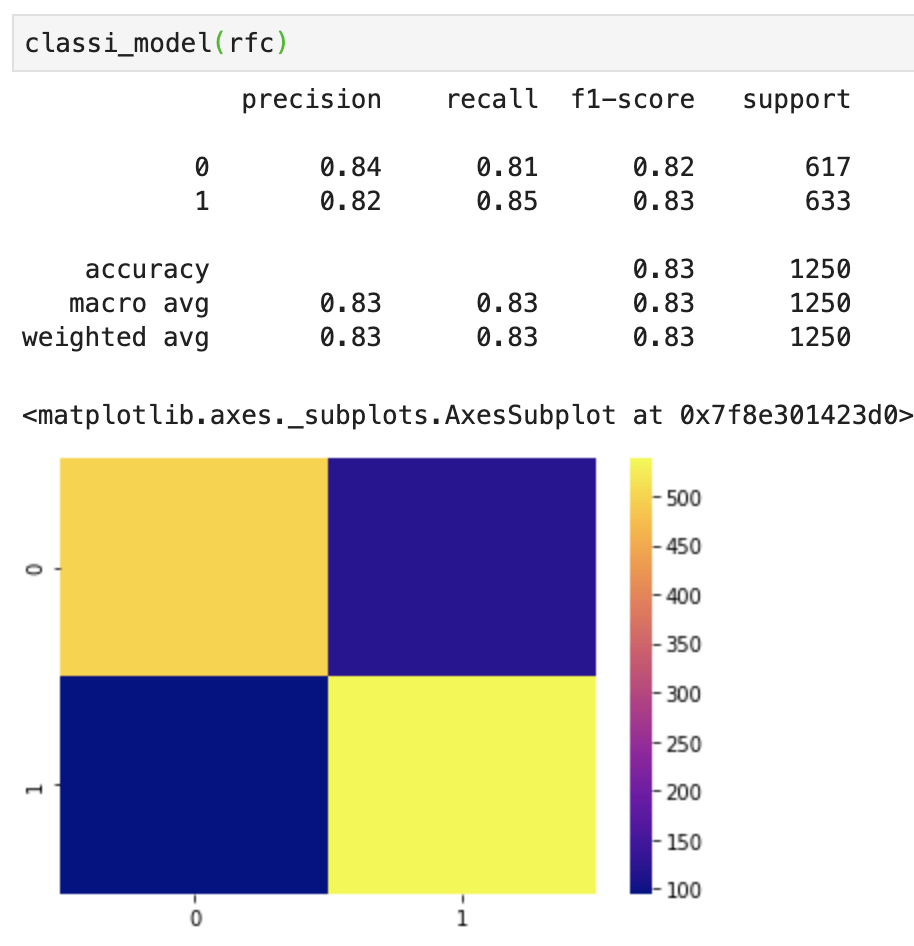
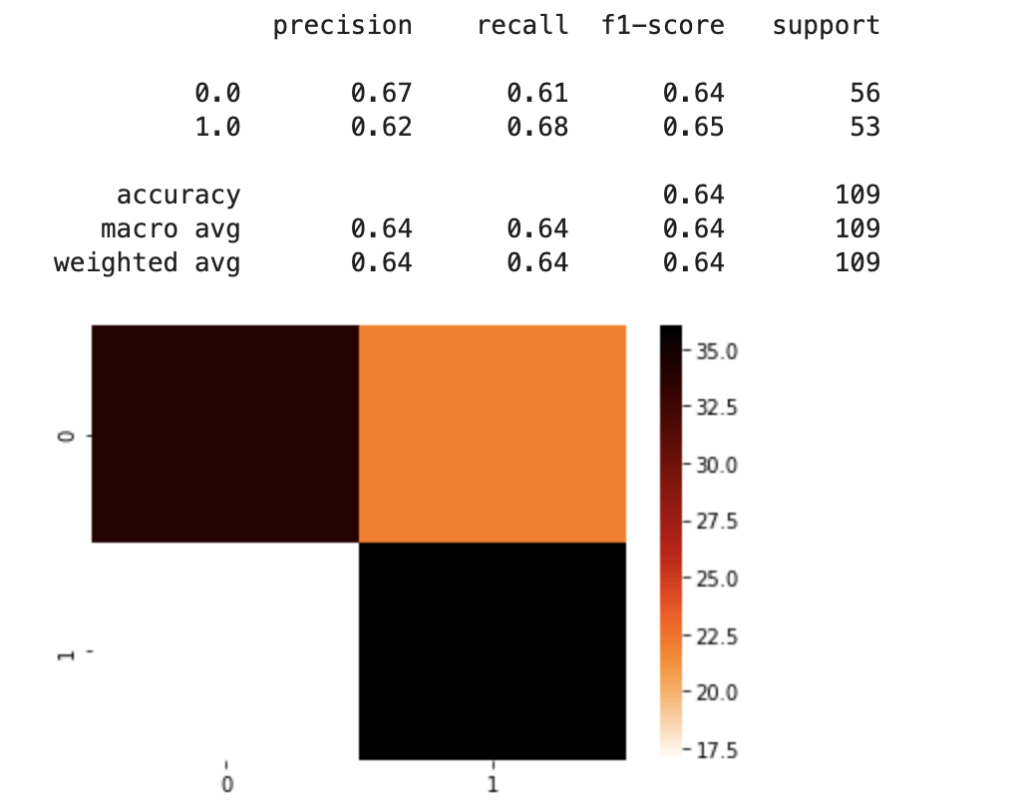
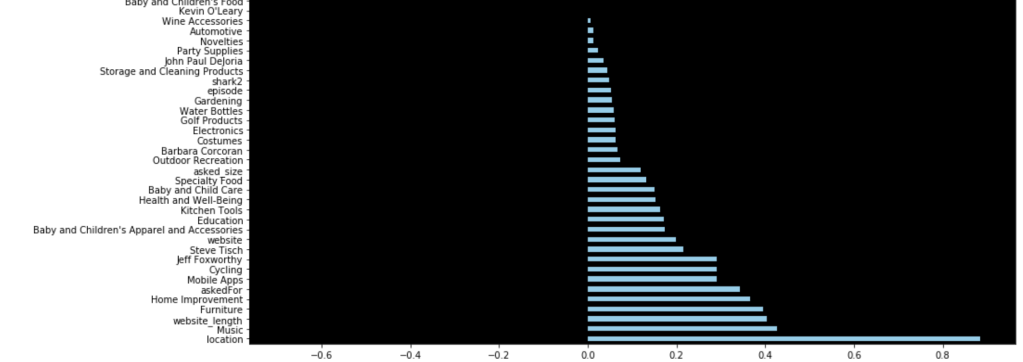
First things first – I need to upsample data. My data was pretty evenly balanced but needed minor adjustments. If you don’t know what I mean by target feature imbalance, check out my blog (on Towards Data Science) over here. Anyway, here comes my best model (notice the features I chose to include):

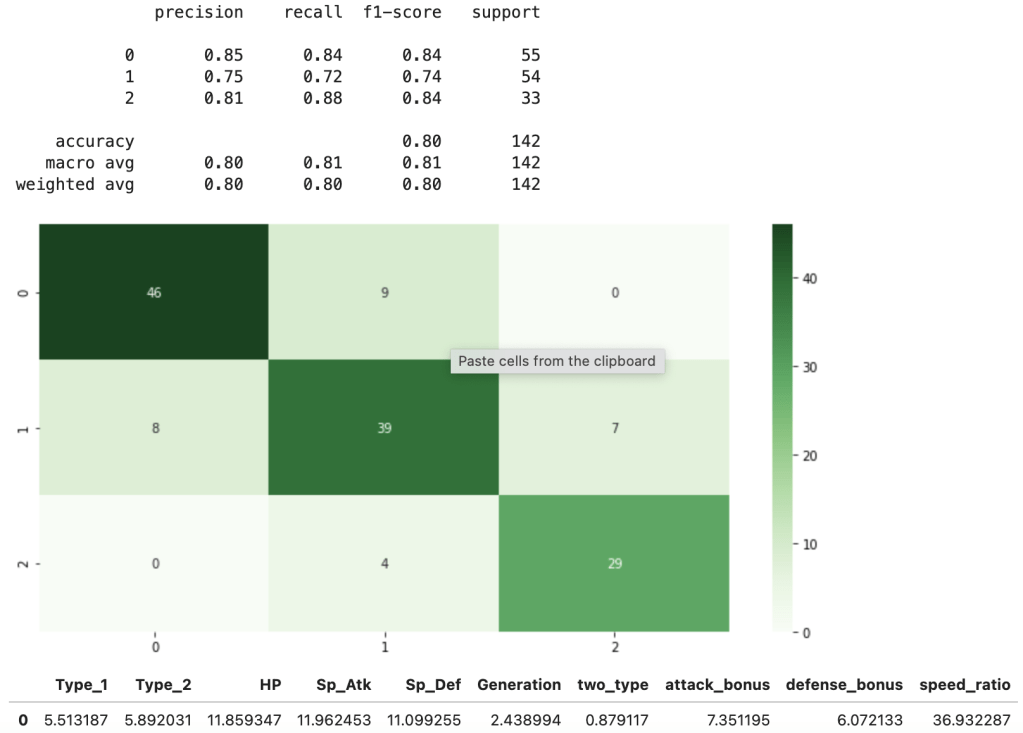
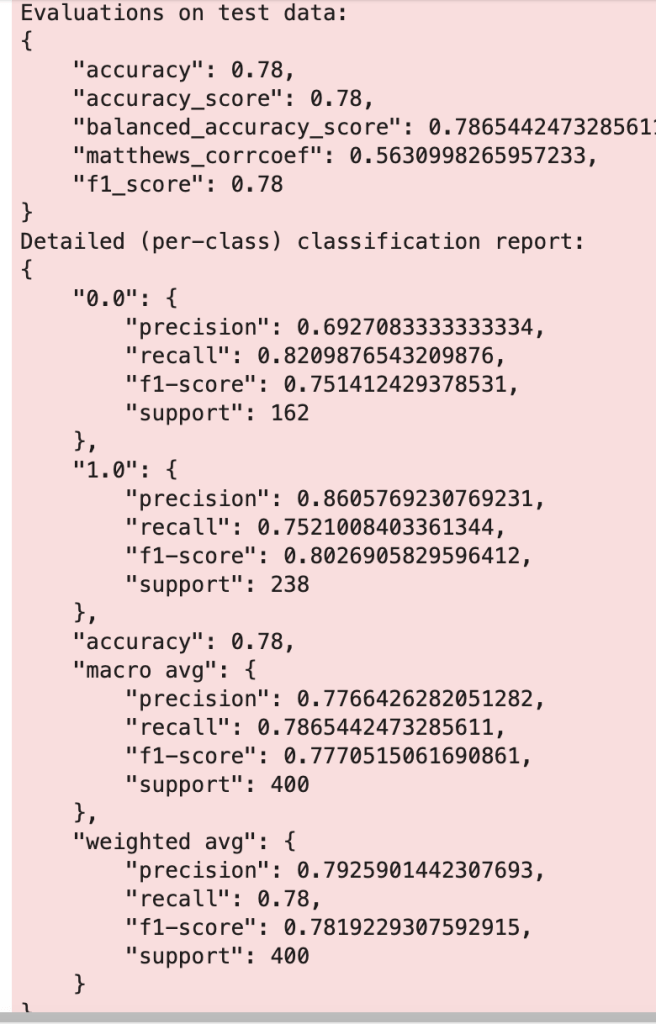
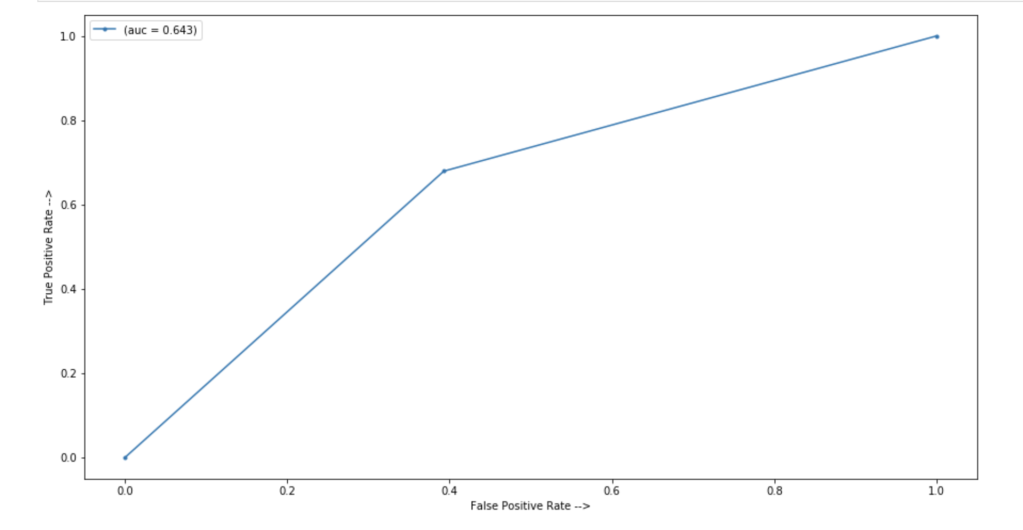
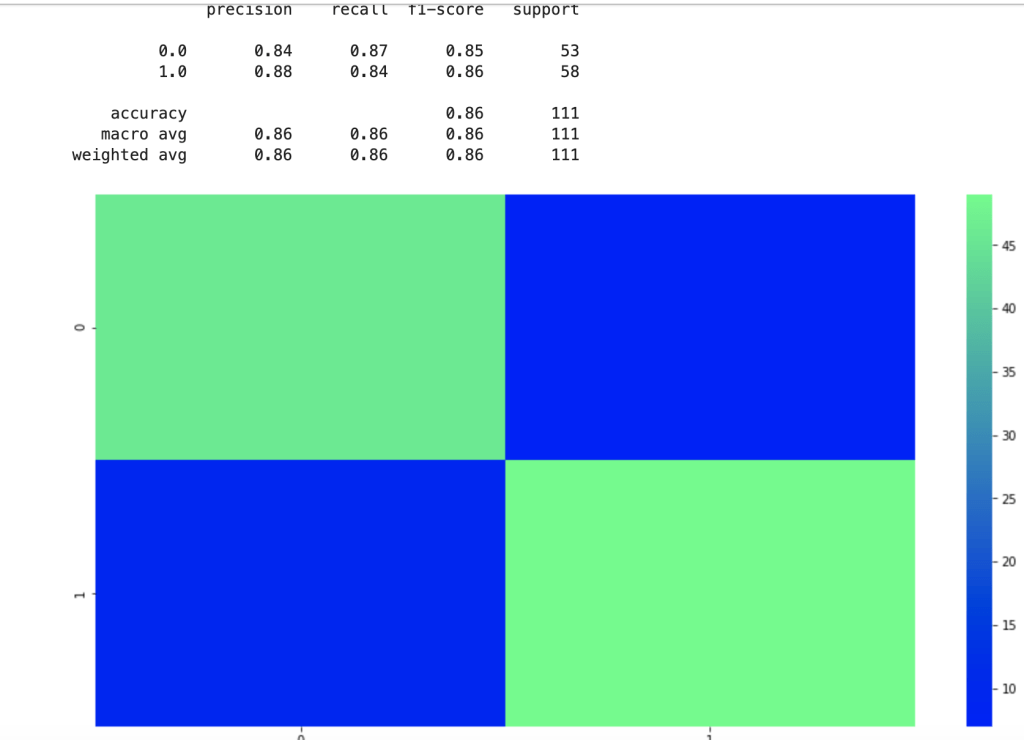
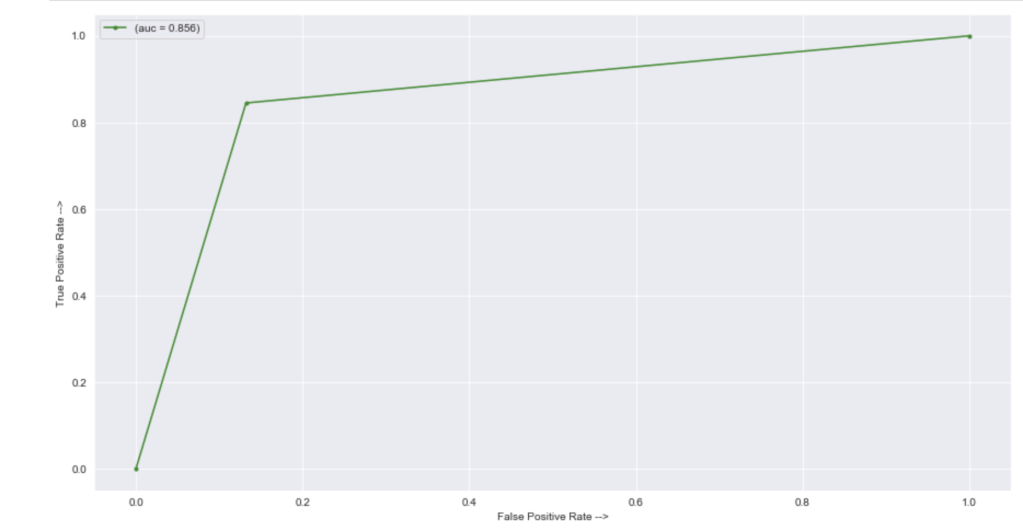
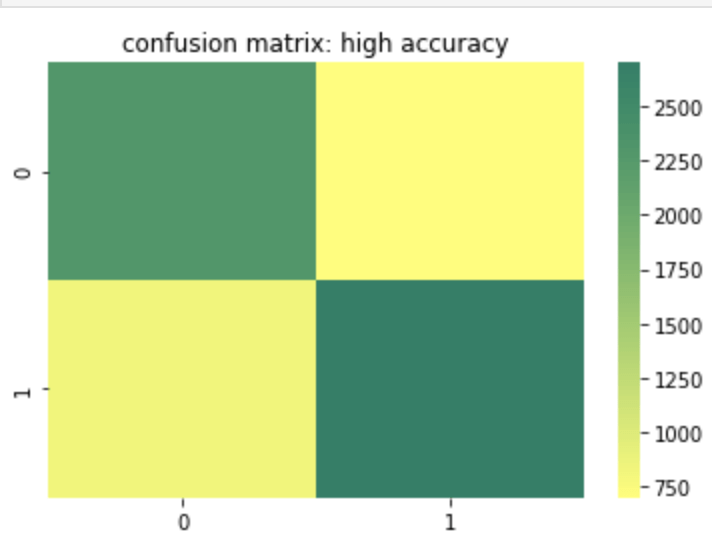
This shows a strong accuracy at 80% along with a good confusion matrix and interesting feature importances. For more information on what the metrics above, such as recall, actually mean, check out my blog over here.

Next Steps

One-Hot Encoding. I think it would be interesting to learn more about which specific types are the strongest. I plan to update this blog after that analysis so stay tuned.

Neural Network. I would love to run a neural network for both the continuous and discrete case.

Polynomial Model. I would also love to see if polynomial features improve accuracy (and possibly help delete the speed-related features).

Conclusion

For all you Pokémon fans and anyone else who enjoys this type of analysis, I hope you liked reading this post. I’m looking forward to the next 25 years of Pokémon.

Introductory NLP Models

Posted on March 5, 2021 by josephcohen94

Building your first Natural Language Processing-based classification model.

Thanks for stopping by today!

Introduction

A popular and exciting application of data science programming is understanding language and the way people speak. Natural Language Processing (NLP) is a field within data science that examines all things language-related. This could be assigning a movie rating from 1-10 based on a review, determining whether an email is or is not spam, gauging sentiment across a span of song lyrics or an opinion article, and anything else you can think of. It’s interesting to transform a sentence, like “the weather is nice today” into an outcome or classification. We can deconstruct this sentence first by taking out words like “the” and “is” that don’t really matter. Next we probably don’t need the word “weather” if it’s understood that we are discussing the weather. So what we’re left with is “good today.” That tells us something about the moment, it has good weather. and that it is not necessarily indicative of the rest of the week or month. This is a really simple sentence and can probably be deconstructed in other ways as well. A more interesting sentence is the following movie review: “the movie wasn’t good.” Let’s repeat our process: delete the words “the” and “movie.” Next we have the word “wasn’t,” a word that implies some sort of negation, and the word “good,” which implies a positive sentiment. Conveniently, we can build and train models to investigate groups of text and come away with solutions at high accuracies. Today’s post will be a basic walkthrough of what can be an introductory model for NLP.

Goals and Data Source

For this post on an introduction to NLP, we will investigate movie reviews and try to predict whether a review is or is not a positive review. My data can be found on kaggle.com and contains only 2 important features. The data describes texts and labels. Label 1 means a good review and label 0 means a bad review. Let me add a quick note before we get started with all the code: I’m not so familiar with NLP projects and am not great or as creative with NLP. I say this not as a disclaimer but rather to show readers that setting up and solving NLP-based projects is not as difficult or complex as it may seem (but yeah – it’s not that easy).

Coding Process

Setup

The setup above should look pretty simple. We import some packages to get going. If you don’t know all these libraries, I won’t waste your time and will focus on the ones that matter most. Pandas is basically Microsoft Excel and spreadsheets for python. The line that begins “df=…” is loading our data into a Pandas spreadsheet (called a “dataframe”). “re” and “string” are two libraries that will help in dealing with text. We will further explain their use when appropriate. “nltk” is Natural Language Toolkit and it is a popular library in dealing with NLP problems. The “lemmatizer” object is a package found in a sub-module of nltk that is used to identify the root of words. There are other options to accomplish this task but the idea is that when we investigate a sentence we want to stop getting confused by similar words. Example: “I am posting posts which will later be posted and re-posted following each post.” Ok, so this sentence doesn’t make a whole lot of sense, but it demonstrates a point; this sentence is talking about posts. We have 5 different words which are all related to the word “post.” Why create a new way to read each unique version of the word “post” when we can just create the following sentence: “I am post post which later be post and post following each post.” The sentence makes even less sense but we still know that this sentence is talking about posts. That’s the idea; work with as few words as possible without losing context or meaning. For more information on the backend work, you can click here. Finally, wordnet is sort of like a dictionary-type resource found in nltk. I’ll give you a quick example to show what I mean.

Cool 😎

Data Prep Functions

To get started here, I am going to minimize this data set using pd.DataFrame().sample(n) with n = 5000. This way my code will take less time and memory to run. I am going to cut my data from 40k rows to only 5k rows. Usually, having more data leads to more accurate models. However, seeing as this is more of an instructive post, I’m going to keep things a bit less computationally heavy. Note that it’s important to reset the index, by the way.

Next, we’ll take a look at “regular expressions,” commonly described as “regex.” Regex is basically “a sequence of characters that define a search pattern,” to quote Wikipedia. Regex is primarily used to process different parts of a sentence and identify things like numbers, punctuation, or other things. For example, if we had the following sentence: “Oh my god, we’re having a fire sale!” – we can understand this sentence without the exclamation mark. The punctuation makes the sentence a bit more interesting, but for computer processing purposes, it’s just added noise. Regex is a bit of a strange resource in syntax and code but I will describe all the regex patterns we will see in our function in a visual. (For more information I found this resource)

We will actually need to add one further cleaning function before we can start lemmatizing words. The function below get’s rid of quotes, empty lines, and single characters sitting in sentences.

For the next function we build, we are going to reduce the amount of words we see using a lemmatization process. Before we can do that, however, we will need to understand how nltk assigns tags. Let’s give an example:

Ok, let’s break this down. First things first, forget every letter after the first letter. Next, figure out what ‘VB’ and ‘NN’ mean. According to this resource, “NN” indicates a noun while “VB” indicates a verb. These tags will help us understand how the lemmatizer should take action. We’ll see more tags in our function:

Now that we can access word tags with a default value set in mind, we need to lemmatize our words. This function is quick.

So let’s take a look at what all this accomplished. We started with something like this:

And now…

It doesn’t look so pretty, but it’s definitely an improvement.

EDA

In short, we will not be doing much EDA. There’s a lot of interesting EDA that can be done with NLP projects. This post is more about building a classification model and we will therefore skip EDA. (Disclaimer EDA can and usually does help build better models – but we are keeping things basic here). If you want to see a fun blog about custom word clouds check out my post here.

Transforming Text To Numbers

Now that we cleaned up are text, we need to turn text into something that computers can understand; numbers. Count vectorizers allow us to accomplish this text. In a short amount of code we can turn a single entry of text into a row whose features are words and the frequency the words appear per text. Let’s say we had the following two sentences; 1) The weather is nice. 2) The weather isn’t cold. So for these two sentences we have 6 total unique words which leads to a data frame including 6 features (not including the classification label). Let’s see some code.

What we see above is the import and instantiation of a count vectorizer which is then applied to the text and exported to a data frame. We also add the label as an additional column. What we see in the data frame is weird. We see words like “aaaaaaah” and “aaa.” However, these words don’t appear in the first 5 lines of data and I would imagine they are statistical outliers. We don’t really see any normal words above and that’s why we see a bunch of zeros.

Stopwords

Believe it or not, we have more data cleaning. A lot of people probably filter out stop-words earlier but I like to do it once we create a data frame. What are stop words? Glad you asked! Stop words are words that “don’t matter” as I like to say it. Stop words could be basic like “the,” “and,” and “it” or situational like “movie,” “film,” or “viewing” in our case. Python has libraries that actually give you sets of stop words. Let’s take a look. Notice how we have to specify the language.

Now I know said no EDA, but I’ll share with you one quick visual.

This visual screams out: “we need more stop words!” Also… what the heck is “br?”

I created the code below to delete the 194 words listed in stop_words if they appear as columns in our data:

We still have a pretty even distribution of good reviews to bad reviews.

Models

So we are basically done with the core data prep and can now run some models. Let’s start with assigning X and Y and doing a classic train-test-split.

Let’s import and instantiate some models…

Let’s create a function to streamline evaluation…

Let’s run a random forest classifier model…

Now that’s pretty good. If some of these metrics look confusing, I recommend you view my blog here that describes machine learning metrics and confusion matrices. At this point in a classification model I like to look at feature importance. We have over 42k features, so we’re definitely not doing feature importance. Let’s focus on what matters. We just built a strong NLP classification model using 5000 data points.

Conclusion

NLP projects take a lot of planning and attention to detail. That said, there is a lot of depth potentially available in NLP projects and having a good knowledge of NLP can help you perform interesting and advanced analysis. NLP is not as easy to learn and implement as some more “basic” low-dimensionality models but NLP is a highly valuable and impressive skill to hold. I hope this post helps readers conduct their own NLP analysis.

Dealing With Imbalanced Datasets The Easy Way

Posted on October 30, 2020 by josephcohen94

Imposing data balance in order to have meaningful and accurate models.

Understanding Imbalances - Chess Forums - Chess.com

Introduction

Thanks for visiting my blog today!

Today’s blog will discuss what to do with imbalanced data. Let me quickly explain what I’m talking about for all you non-data scientists. If I am screening people too see if they have a disease and I accurately screen every single person (let’s say I screen 1000 people total). Sounds good, right? Well, what if I told you that 999 people had no issues and I predicted them as not having a disease. The other 1 person had the disease and I got it right. This clearly holds little meaning. In fact, I would basically hold just about the same level of overall accuracy if I had predicted this diseased person to be healthy. There was literally one person and we don’t really know if my screening tactics work or I just got lucky. In addition, if I were to have predicted this one diseased person to be healthy, then despite my high accuracy, my model may in fact be pointless since it always ends in the same result. If you read my other blog posts, I have a similar blog which discusses confusion matrices. I never really thought about confusion matrices and their link to data imbalance until I wrote this blog, but I guess they’re still pretty different topics since you don’t normally upsample validation data, thus giving the confusion matrix its own unique significance. However, if you generate a confusion matrix to find results after training on imbalanced data, you may not be able to trust your answers. Back to the main point; imbalanced data causes problems and often leads to meaningless models as we have demonstrated above. Generally, it is thought that adding more data to any model or system will only lead to higher accuracy and upsampling a minority class is no different. A really good example of upsampling a minority class is fraud detection. Most people (I hope) aren’t committing any type of fraud ever (I highly recommend you don’t ask me about how I could afford that yacht I bought last week). That means that when you look at something like credit card fraud, the majority of the time a person makes a purchase, their credit card was not stolen. Therefore, we need more data on cases when people are actually the victims of fraud to have a better understanding of what to look for in terms of red flags and warning signs. I will discuss two simple methods you can use in python to solve this problem. Let’s get started!

When To Balance Data

For model validation purposes, it helps to have a set of data with which to train the model and a set with which to test the model. Usually, one should balance the training data and leave the test data unaffected.

First Easy Method

Say we have the following data…

Target class distributed as follows…

The following code below allows you to extremely quickly decide how much of each target class to keep in your data. One quick note is that you may have to update the library here. It’s always helpful to update libraries every now and then as libraries evolve.

Look at that! It’s pretty simple and easy. All you do is decide how many of each class to keep. After that, a certain number of rows resulting in one target feature outcome and a certain number of rows resulting in an alternative target feature outcome remain. The sampling strategy states how many rows to keep from each target variable. Obviously you cannot exceed the maximum per class, so this can only serve to downsample, which is not the case with our second easy method. This method works well when you have many observations from each class and doesn’t work as well when one class has significantly less data.

Second Easy Method

The second easy method is to use resample from sklearn.utils. In the code below, I decided to point out that I was using train data as I did not point it out above. Also in the code below, I generate new data of class 1 (sick class) and artificially generate enough data to make it level with the healthy class. So all the training data stays the same, but I repeat some rows from the minority class to generate that balance.

Here are the results of the new dataset:

As you can see above, each class represents 50% of the data. This method can be extended to cases with more than two classes quite easily as well.

Update!

If you are coming back and seeing this blog for the first time, I am very appreciative! I recently worked on a project that required data balancing. Below, I have included a rough but good way to create a robust data balancing method that works well without having to specify the situation or context too much. I just finished writing this function but think it works well and would encourage any readers to take this function and see if they can effectively leverage it themselves. If it has any glitches, I would love to hear feedback. Thanks!

Conclusion

Anyone conducting any type of regular machine learning modeling will likely need to balance data at some point. Conveniently, it’s easy to do and I believe you shouldn’t overthink it. The code above provides a great way to get started balancing your data and I hope it can be helpful to readers.

Thanks for reading!

Basic AutoGluon Models

Posted on September 25, 2020 by josephcohen94

Learning the basics of a useful AutoML library

GitHub - awslabs/autogluon: AutoGluon: AutoML Toolkit for Deep Learning

Introduction

Thank you for visiting my blog today!

Recently, I was introduced to an interesting library geared toward building fast and accurate machine learning models using a library called AutoGluon. I don’t claim credit for any of the fancy backend code or functionality. However, I would like to use this blog as an opportunity to quickly introduce this library to anyone (and I imagine that includes most people who are data scientists) and show a quick modeling process. A word I used twice in the past sentence was “quick.” As we will see, that is the one of the best parts of AutoGluon.

Basic Machine Learning Model

In order to evaluate whether AutoGluon is of any interest to me (or my readers), I’d like to first discuss what I normally want from an ML model. For me, outside of things like EDA, hypothesis testing, or data engineering, I am mainly looking for two things at the end of the day; I want the best possible model in terms of accuracy (or recall or precision) and also want to look at feature importances as that is often where the interesting story lies. How we set ourselves up to have a good model that can accomplish these two tasks in the best way possible is another story for another time and frankly it would be impossible to tell that entire story in just one blog.

An autogluon Model Walkthrough

So let’s see this in action. I will link the documentation here before I begin: (https://autogluon.mxnet.io/). Feel free to check it out. Like I said, I’m just here today to share this library. First things first though: my data concerns wine quality using ten predictive features. These features are citric acid, volatile acidity, chlorides, density, pH level, alcohol level, sulphates, residual sugar, free sulfur dioxide, and residual sulfur dioxide. It can be found at (https://www.kaggle.com/uciml/red-wine-quality-cortez-et-al-2009). This data set actually appears in my last blog on decision trees.

Ok, so the next couple lines are fairly standard procedure, but I will explain them:

Basically, I am loading all my functions, loading my data, and splitting my data into a set for training a model and a set for validating a model.

Here comes the fun stuff:

So this looks pretty familiar to a data scientist. We are fitting a model on data and passing the target variable to know what is being predicted. Here is some of the output:

That was fast. We also what models worked best.

Now let’s introduce new data:

Output:

Whoa is right, it looks we just entered The Matrix. Ok… this is really not that complex, so let’s just take one more step:

Output:

Ok, now that makes a bit more sense.

We can even look backward and check on how autogluon interpreted this problem:

We have a binary outcome of 0 or 1 containing features that are all floats (numbers that are not necessarily whole).

What about feature importance?

So we see our feature importances above, and run time also. This library is big on displaying run times.

Conclusion

AutoGluon is an impressive python library that can accomplish many different tasks in a short amount of time. You can probably optimize your results by doing your cleaning and preprocessing, I would imagine. Whether this means upsampling a minority class or feature selection, you still have to do some work. However, if you are looking for a quick and powerful library, AutoGluon is a great place to start.

Thanks for Reading!

Thank You Text On Binary Stock Footage Video (100% Royalty-free) 27866767 | Shutterstock

Decision Trees, Part 2

Posted on September 18, 2020 by josephcohen94

Using a sample data set to create and test a decision tree model.

What Are Some Fast-Growing Trees for California Properties? - Evergreen Arborist Consultants

Introduction

Welcome to my blog and thanks for dropping by!

Today, I have my second installment in my decision tree blog series. I’m going to create and run a model leveraging decision trees using data I found on a public data repository. Hopefully you saw part one in this series as it will be pretty important. For a quick reminder, I am going to use the gini metric to make my tree. Let’s begin!

Data Preparation

My data concerns wine quality. I picked this data set because it was a relatively basic data set and was pretty clean to begin. My only important preprocessing was running feature selection to cut down from ten features to five predictive feature. I also binned all my features as either a zero or one to make life easier. That means that instead of having a continuous measure between, say 1 and 100, it instead becomes 0 for lower and 1 for higher. Thankfully, this did not sacrifice model accuracy that much. Also, just to keep things simple, I decided to only look at 150 rows of data so things don’t get out of control. I also wrote the following function for calculating gini:

Here is a function that is built on top of that function just to make things a bit easier (it was cut off a bit):

The function above will allow me to easily go into different branches of each tree while doing very little manual computer programming.

Anyway, this is going to get a little messy I imagine. I will use my functions to skip the annoying calculations and data manipulation, but there are still going to be a lot of branches. Therefore, I will try to provide a picture of my hand-typed tree. (I found this link for how to create a visualization using python: https://towardsdatascience.com/visualizing-decision-trees-with-python-scikit-learn-graphviz-matplotlib-1c50b4aa68dc).

By the way… here is a preview of my data containing five predictive features:

Building My Tree

Let’s start with the base gini values for the five predictive features in terms of their effect on the target feature of quality.

Now, we enter the volatile acidity 0 and volatile acidity 1 worlds:

Ok, so what does all this mean? Assuming we take the value of zero for volatile acidity, and as we’ll see – that is the far more interesting path, our next branch to look at would be pH. Afterward we dive into pH 1 and pH 0 and so on…

Now that we have got a feel of what this tree is going to look like in terms of how we set up our calculations along each branch, I am going to just do the rest by myself and post some final results. There are going to be a lot of branches and looking at every single one will get boring very quickly.

A couple notes:

One: part of this project involved upsampling a minority target class. I did a whole lot of work and basically finished my tree but had to do it all over again because of target class imbalance. Don’t neglect about this key part of the modeling process (if necessary) or your models will be incomplete and inacurate!

Two: I am going to post my model in the form of an Excel table showing all the paths of the tree. You will most likely have no way of knowing this, unless you look at the data (https://www.kaggle.com/uciml/red-wine-quality-cortez-et-al-2009) and go through the same pre-processing I did (which was rather non-traditional), but not all the subsets displayed actually exist. So I will have some branches from the tree written out in my Excel table that are not actually part of any tree at all. When that happens, I took a step back and just saw what things would look like in the absence of that feature. Some combinations of characteristics of wine (that’s what my data concerns) don’t exist in the 150 rows I chose at random to build my tree. Consequently, when you view my tree, you should focus on the order of features as opposed to the particular combinations, as I imagine that I will end up listing every possible combination possible. The order that the features appear tell the story of what feature was most predictive at each branch. Don’t get lost in all the details.

Here is what I came up with (I color coded each feature to make it easy to follow):

In case you are wondering, the first feature in my tree, volatile acidity, was so predictive that any time it was equal to 1, the conclusion was 0 for the target variable.

So now it’s time to see if this actually works; we need test data. I used a basic train-test-split. That’s data science for language for artificially separating data to specifically not build a model on and instead use for testing purposes. I’ll be transparent and display my test data set. At this point, I don’t know how well my model is going to work so we’re all in this together in a sense.

So now that we have the logic in place and you have seen all my test data, you could theoretically “run the model” yourself and follow each path outlined above and see how the data fits in. That sounds like a lot of work, though. Here is what it would look like if you did all that work:

At 68% accuracy, I am proud of this model. If we eliminate the binary binning and add more of the original data, this number will go up to ~77%.

Conclusion

Using the gini metric and a real data set (and a little bit of preprocessing magic), we were able to create a basic decision tree. Considering the circumstances, it was fairly accurate. Decision trees are great because they are fairly simple conceptually and the math is not that hard either.

Thanks for reading!

Tree of Life Bar Mitzvah Invitation Set | Lemon Leaf Prints

Decision Trees, Part 1

Posted on September 10, 2020 by josephcohen94

Understanding how to build a decision tree using statistical methods.

European Tree of the Year – The Witch Tree - The Netherlands

Introduction

Thanks for visiting my blog today!

Life is complex and largely guided by the decisions we make. Decisions are also complex and are usually the result of a cascade of other decisions and logic flowing through our heads. Just like we all make various decision trees in our heads (whether we actively think about them or not) to guide our decisions, machines can also leverage a sequence of decisions (based on logical rules) to come to a conclusion. Example: I go to a Blackhawks game. The Blackhawks are tied with 2 minutes left. It’s a preseason game. Do I leave early to avoid the parking lot they call “traffic” and catch the rest on TV or radio, or do I stay and watch a potential overtime game (which is always exciting). There’s nothing on the line for the Blackhawks (and therefore their fan base) but I paid money and took a chunk of time out of my day to see Patrick Kane light up the scoreboard and sing along to Chelsea Dagger. There are few experiences that are as exciting as a last second or overtime / extra-time game winning play and I know from past live experience. Nevertheless, we are only scratching the surface of what factors may or may not be at play. What if I am a season ticket holder? I probably would just leave early. What if I come to visit my cousins in Chicago for 6 individual (and separate) weeks every year? I might want to stay as it’s likely that some weeks I visit there won’t even be a game. Right there, I built a machine learning model in front of your eyes (sort of). My de-facto features are timeInChicago, futureGamesAttending, preseasonSeasonPosteason, timeAvailable, gameSituation. (These are the ones I made up after looking back at build-up to this point and think they work well – I’m sure others will think of different ways to contextualize this problem). My target feature can be binary; stay or leave. It can also be continuous; time spent at game. It can also be multi-class; periods stayed in (1, 2, or 3). This target feature ambiguity can change the problem depending on one’s philosophy. Whether you realize this or not, you are effectively creating a decision tree. It may not feel like all these calculations and equations are running through your head and you may not even take that long or incur that much stress when making a decision, but you’re using that decision tree logic.

In today’s blog we are going to look at the concepts surrounding a decision tree and discuss how they are built and make decisions. In my next blog in this series (which may or may not be my next blog I write), I will take the ideas discussed here and show an application on real-world data. Following that, I will build a decision tree model from scratch in python. The blog after that will focus on how to take the basic decision tree model to the next level using a random forest. After that blog, I will show you how to leverage and optimize decision trees and random forests in machine learning models using python. There may be more on the way, but that’s the plan for now.

I’d like to add that I think I’m going to learn a lot myself in this blog as it’s important, especially during a job interview, to explain concepts. Many of you who may know python may know ways to quickly create and run a decision tree model. However, in my opinion, it is equally as important (if not more) to understand the concepts and to be able explain what things like entropy and information gain are (some main concepts to be introduced later). Concepts generally stay in place, but coding tends to evolve.

Let’s get to the root of the issue.

Bihar govt launches 'Pyaar ka Paudha' campaign to encourage practice of planting trees | India News | Zee News

How Do We Begin?

It makes sense that we want to start with the most decisive feature. Say a restaurant only serves ribeye steak on Monday. I go to the restaurant and have to decide what to order, and I really like ribeye steak. How do I begin my decision tree? The first thing I ask myself is if it’s Monday or not. If it’s Monday, I will always get the steak. Otherwise, I won’t be able to order that steak. In the non-Monday universe, aka the one where I will be guaranteed to not get the steak, the whole tree changes when I pick what to eat. So we want to start with the most decisive features and work our way down to the least decisive features. Sometimes the trees will not have the same branches at the same time. Say the features (in this restaurant example) are day of the week, time of day, people with me eating, and cash in my pocket. Now I really like steak. So much so that every Monday I am willing to spend any amount of money for the ribeye steak (I suppose in this example, the cost is variable). For other menu items, I may concern myself with price a bit more. Price doesn’t matter in the presence of value but becomes a big issue in the absence of value. So, in my example: money in pocket will be more decisive in the non-Monday example than the Monday example and therefore find itself at a different place in the tree. The way this presents itself in the tree is that 100% of the times it is Monday and I have the cash to pay for the steak I will pay for it and 100% of the time I don’t quite have enough in my pocket I will have to find some other option. That’s how we start each branch of the tree, starting with the first branch.

How Do We Use Math To Solve This Problem?

Debate: Book Ginny Vs Movie Ginny - BookMyShow

There’s a couple ways to go about this. For today, I’d like to discuss gini (pronounced the same as Ginny Weasley from Harry Potter). Gini is a measure of something called impurity. Most of the time, with the exception of my Monday / steak example, we don’t have completely decisive features. Usually there is variance within each feature. Impurity is the amount of confusion or lack of clarity in the decisiveness of a feature. So if we have a feature that has around 50% of the occurrences resulting in outcome 1 and 50% resulting in outcome 2, we have not learned anything exciting. By leveraging the gini statistic, we can understand which of our features is least impure and start the tree with that feature and then continue the tree by having the next branch be whatever is least impure in reference to the previous branch. So here is the equation we have all been waiting for:

Gini Index vs Information Entropy | by Andrew Hershy | Towards Data Science

Here’s a quick example, and then I’ll get back to the equation (I apologize for the rotation):

In the example above, I only compare the target feature to whether it’s rainy or not. There is no conditional probability here on things like time of day or day of week. This implies that we are at (or deciding) the top of the tree and seeing if raininess is as strong a predictive feature as other ones. We see that if we assume it is rainy, our gini impurity, as measured by one minus the probability of yes and the probability of no (both squared), sits around 0.32. If it is not a rainy day, the gini impurity is a bit higher, meaning we don’t have as much clarity as to whether or not I will go to the gym. In the weighted average result of 0.38, we see that this number is close to 0.4 than 0.32 because most days are not rainy days. In my opinion, using this data generated on the spot for demonstration purposes, the gini impurity for raniness is quite high and therefore would not sit at the top of the tree. It would be a lower branch. This concept is not exclusive to the binary choice, however it presents itself differently in other case. Say we want to know if I go to the gym based on how much free time I have in my day and my options include a range of numbers such as 60 minutes, 75 minutes, 85 minutes, and other values. To decide how we split the tree, we create “cutoff” points (corresponding to each value – so we create a cutoff at over 67.5 minutes and below 67.5 minutes followed by testing the next cutoff at over 80 minutes and below 80 minutes) to find the “cutoff” point with the least impurity. In other words, if we assume that the best way to measure whether I go or not is by deciding if I have more than 80 minutes free or less than 80 minutes free, than the tree goes on to ask if I have more than 80 minutes or less than 80 minutes. I also think this means that the cutoff point can change in different parts of the tree. For example, the 80 minute concept may be important on rainy days but I may go to the gym even with less free time on sunny days. Note that the cutoff always represents a binary direction forward. Basically we keep following the decision tree down using gini as a guide until we get to the last feature. At that point we just use the majority to decide.

Conclusion

Decision trees are actually not that complex, they can just take a long time when you have a lot of data. This is great to know and quite comforting considering how fundamental they implicitly are to everyday life. If you’re ever trying to understand the algorithm, explain it in an interview, or make your own decision tree (for whatever reason…), I hope this has been a good guide.

Thanks for reading!

Palm Trees Thank You Card by REVEL & Co.

Sink or Swim

Posted on September 4, 2020 by josephcohen94

Effectively Predicting the Outcome of a Shark Tank Pitch

Introduction

Thank you for visiting my blog today!

Recently, during my quarantine, I have found myself watching a lot of Shark Tank. In case you are living under a rock, Shark Tank is a thrilling (and often parodied) reality TV show (currently on CNBC) where hopeful entrepreneurs come into the “tank” and face-off against five “sharks.” The sharks are successful entrepreneurs who are basically de-facto venture capitalists looking to invest in the hopeful entrepreneurs mentioned above. It’s called “Shark Tank” and not something a bit less intimidating because things get intense in the tank. Entrepreneurs are “put through the ringer” and forced to prove themselves worthy of investment in every way imaginable while standing up to strong scrutiny from the sharks. Entrepreneurs need to demonstrate that they have a good product, understand how to run a business, understand the economic climate, are a pleasant person to work with, are trustworthy, and the list goes on and on. Plus, contestants are on TV for the whole world to watch and that just adds to the pressure to impress. If one succeeds, and manages to agree on a deal with a shark (usually a shark pays a dollar amount for a percentage equity in an entrepreneur’s business), the rewards are usually quite spectacular and entrepreneurs tend to get quite rich. I like to think of the show, even though I watch it so much, as a nice way for regular folks like myself to feel intelligent and business-savvy for a hot second. Plus, it’s always hilarious to see some of the less traditional business pitches (The “Ionic Ear” did not age well: https://www.youtube.com/watch?v=FTttlgdvouY). That said, I set out to look at the first couple seasons of Shark Tank from a data scientist / statistician’s perspective and build a model to understand whether or not an entrepreneur would succeed or fail during their moment in the tank. Let’s dive in!

Data Collection

To start off, my data comes from kaggle.com and can be found at (https://www.kaggle.com/rahulsathyajit/shark-tank-pitches). My goal was to predict the target feature “deal” which was either a zero representing a failure to agree on a deal or a 1 for a successful pitch. My predictive features were (by name): description, episode, category, entrepreneurs, location, website, askedFor, exchangeForStake, valuation, season, shark1, shark2, shark3, shark4, shark5, episode-season, and Multiple Entrepreneurs. Entrepreneurs meant the name of the person pitching a new business, asked for means how much money was requested, exchange for stake represents percent ownership offered by the entrepreneur, valuation was the implied valuation of the company, shark1-5 is just who was present (so shark1 could be Mark Cuban or Kevin Harrington, for example), and multiple entrepreneurs was a binary of whether or not there were multiple business owners beforehand. I think those are the only features that require explanation. I used dummy variables to identify which sharks were present in each pitch (this is different from the shark1 variable as now it says Mark Cuban, for example, as a column name with either a zero or one assigned depending on whether or not he was on for that episode) and also used dummy variables to identify the category of each pitch. I also created some custom features. Thus, before removing highly correlated features, my features now also included the dummy variables described above, website converted to a true-false variable depending on whether or not one existed, website length, a binned perspective on the amount asked for and valuation, and a numeric label identifying which unique group of sharks sat for each pitch.

EDA (Exploratory Data Analysis)

The main goal of my blog here was to see how strong of a model I could build. However, an exciting part of any data-oriented problem is actually looking at the data and getting comfortable with what it looks like both numerically and visually. This allows one to easily share fun observations, but also provides context on how to think about some features throughout the project. Here are some of my findings:

Here is the distribution of the most common pitches (using top 15):

Here is the likelihood of getting a deal by category with an added filter for how much of a stake was asked for:

Here are some other relationships with the likelihood of getting a deal:

Here are some basic trends from season 1 to season 6:

Here is the frequency of each shark group:

Here are some other trends over the seasons. Keep in mind that the index starts at zero but that relates to season 1:

Here is the average stake offered by leading categories:

Here comes an interesting breakdown of what happens when there is and is not a guest shark like Richard Branson:

Here is a breakdown of where the most common entrepreneurs come from:

In terms of the most likely shark group for people from different locations:

I also made some visuals of the amount of appearances of each unique category by each of the 50 states. We obviously won’t go through every state. Here are a couple, though:

Here is the average valuation by category:

Here is a distribution of pitches to the different shark groups (please ignore the weird formatting):

Here come some various visuals related to location:

Here come some various visuals related to shark group

This concludes my EDA for now.

Modeling

After doing some basic data cleaning and feature engineering, it’s time to see if I can actually build a good model.

First Model

For my first model, I used dummy variables for the “category” feature and information on sharks. Due to the problem of having different instances of the category feature, I split my data into a training and test set after pre-processing the data. I mixed and matched a couple of scaling methods and machine learning classification models before landing on standard scaling and logistic regression. Here was my first set of results:

In terms of an ROC/AUC visual:

64% accuracy on a show where anything can happen is a great start. Here were my coefficients in terms of a visual:

Let’s talk about these results. It seems like having Barbara Corcoran as a shark is the most likely indicator of a potential deal. That doesn’t mean Barbara makes the most deals. Rather, it means that you are likely to get a deal from someone if Barbara happens to be present. I really like Kevin because he always makes a ridiculous offer centered around royalties. His coefficient sits around zero. Effectively, if Kevin is there, we have no idea whether or not there will be a deal. He contributes nothing to my model. (He may as well be dead to me). Location seems to be an important decider. I interpret this to mean that some locations appear very infrequently and just happened to strike a deal. Furniture, music, and home improvement seem to be the most successful types of pitches. I’ll let you take a look for yourself to gain further insights.

Second Model

For my second model, I leveraged target encoding for all categorical data. This allowed me to split up my data before any preprocessing. I also spent time writing a complex backend helper module to automate my notebook. Here’s what my notebook looked like after all that work:

That was fast. Let’s see how well this new model performed given the new method used in feature engineering:

There is clearly a sharp and meaningful improvement present. That said, by using target encoding, I can no longer see the effects of individual categories pitched or sharks present. Here were my new coefficients:

These are a lot less coefficients than in my previous model due to the dummy variable problem, but this led to higher scores. This second model really shocked me. 86% accuracy for predicting the success of a shark tank pitch really surprised me given all the variability present in the show.

Conclusion

I was really glad that my first model was 64% accurate given what the show is like and all the variability involved. I came away with some insightful coefficients to understand what drove predictions. By sacrificing some detailed information I kept with dummy variables, I was able to encode categorical data in a different way which led to an even more accurate model. I’m excited to continue this project and add more data from more recent episodes to continue to build a more meaningful model.

Thanks for reading and I hope this was fun for any Shark Tank fans out there.

Anyway, this is the end of my blog…

Linear Regression, Part 2

Posted on August 21, 2020 by josephcohen94

Building an Understanding of Gradient Descent Using Computer Programming

Gradient Descent - Gradient descent - Product Manager's Artificial ...

Introduction

Thank you for visiting my blog.

Today’s blog is the second blog in a series I am doing on linear regression. If you are reading this blog, I hope you have a fundamental understanding of what linear regression is and what a linear regression model looks like. If you don’t already know about linear regression, you may want to read this blog: https://data8.science.blog/2020/08/12/linear-regression-part-1/ I wrote and come back later. In the blog referenced above, I talk at a high level about optimizing for parameters like slope and intercept. Well, we are going to talk about how machines minimize error in predictive models. We are going to introduce the idea of a cost function soon. Even though we will be discussing cost functions in the context of linear regression, you will probably realize that this is not the only application. That said, the title of this blog shouldn’t confuse anyone and all should understand that gradient descent is more of an overarching subject for many machine learning problems.

The Cost Function

The first idea that needs to be introduced, as we begin to discuss gradient descent, is the cost function. As you may recall, we wrote out a pretty simple calculus formula that found the optimal slope and intercept for the 2D model in the last blog. If you didn’t read last blog, that’s fine. The main idea is that we started with an error function, or MSE. We then took partial derivatives of that function and applied optimization techniques to search for a minimum. What I didn’t tell you in my blog, and people who didn’t read my blog may or may not know is that there is in fact a name for the function that takes a partial derivate in an error function. We call it the cost function. Here is a common representation of the cost function (for 2-dimensional case):

b'Linear Regression using Gradient Descent | nicolasconstanty ...

This function should be familiar. This is basically just the sum of model error in linear regression. Model error is what we try to minimize in EVERY machine learning model, so I hope you see why gradient descent is not unique for linear algebra.

What is a Gradient?

Simply put, a gradient is the slope of a curve, or derivative, at any point on a plane with regards to one variable (in a multivariate function). Since the function being minimized is the loss function, we follow the gradient down (hence the name gradient descent) until it approaches or hits zero (for each variable) in order to have minimal error. In gradient descent, we start by taking big steps and slow down as we get closer to that point of minimal error. That’s what gradient descent is; slowly descending down a curve or graph to the lowest point, which represents minimal error, and finding the parameters that correspond to that low point. Here’s a good visualization for gradient descent (for one variable).

The history of Gradient Descent | Machine Intelligence Academy

The next equation is one I found online that illustrates how we use the graph above in practice:

10 Stochastic Gradient Descent Optimisation Algorithms + Cheat ...

The above two visual may seem confusing, so let’s work backwards. W t+1 corresponds to our next predicted value for optimal coefficient value. W t was our previous assumption for optimal coefficient value. The term on the right looks a bit funky, but it’s pretty simple actually. The alpha corresponds to the learning rate and the quotient is the gradient. The learning rate is essentially a parameter that tells us how quickly we move. If it is low, models can be computationally expensive, but if it is high, it may not hit the best concluding point. At this point, we can revisit the gif. The gif shows the movement in error as we iteratively update W t into W t+1.

At this point, I have sort-of discussed the gradient itself and danced around the topic. Now, let’s address it directly using visuals. Now keep in mind, gradients are partial derivatives for variables in the cost function that enable us to search for a minimum value. Also, for the sake of keeping things simple, I will express gradients using the two-dimensional model. Hopefully, the following visual shows a clear progression from the cost function.

An Introduction to Gradient Descent and Linear Regression

In case the above confuses you, I would not focus on the left side of either the top or bottom equation. Focus on the right side. These formulas should look familiar as they were part of my handwritten notes in my initial linear regression blog. These functions represent the gradients used for slope (m) and intercept (b) in gradient descent.

Let’s review: we want to minimize error and use the derivative of the error function to help that process. Again, this is gradient descent in a simple form:

I’d like to now go through some code in the next steps.

Gradient Descent Code

We’ll start with a simple model:

Next, we have our error:

Here we have a single step in gradient descent:

Finally, here is the full gradient descent:

Bonus Content!

I also created an interactive function for gradient descent and will provide a demo. You can copy my notes from this notebook with your own x and y values to run an interactive gradient descent as well.

Demo link: https://www.youtube.com/watch?v=hWqvmmSHg_g&feature=youtu.be

Conclusion

Gradient descent is a simple concept that can be incredibly powerful in many situations. It works well with linear regression, and that’s why I decided to discuss it here. I am told that often times, in the real world, using a simple sklearn or stastsmodels model is not good enough. If it were that easy, I imagine the demand for data scientists with advanced statistical skills would be lower. Instead, I have been told, that custom cost functions have to be carefully though out and gradient descent can be used to optimize those models. I also did my first blog video for today’s blog and hope it went over well. I have one more blog in this series where I go through regression using python.

Sources and Further Reading

(https://medium.com/meta-design-ideas/linear-regression-by-using-gradient-descent-algorithm-your-first-step-towards-machine-learning-a9b9c0ec41b1)

(https://towardsdatascience.com/the-complete-guide-to-time-series-analysis-and-forecasting-70d476bfe775)

Tips for Writing Professional Thank You Notes | Macaulay Honors ...

Linear Regression, Part 1

Posted on August 12, 2020 by josephcohen94

Acquiring a baseline understanding of the ideas and concepts that drive linear regression.

Introduction

Thanks for visiting my blog!

Today, I’d like to do my first part in a multi-part blog series discussing linear regression. In part 1, I will go through the basic ideas and concepts that describe what a linear regression is at its core, how you create one and optimize its effectiveness, what it may be used for, and why it matters. In part 2, I will go through a concept called gradient descent and show how I would build my own gradient descent, by hand, using python. In part 3, I will go through the basic process of running linear regression using scikit-learn in python.

This may not be the most formal or by-the-book guide, but the goal here is to build a solid foundation and understanding of how to perform a linear regression and what the main concepts are.

Motivating Question

Say we have the following (first 15 of 250) rows of data (it was randomly generated and does not intentionally represent any real world scenario or data):

Graphically, here is what these 250 rows sort of look like:

We want to impose a line that will guide our future predictions:

The above graph displays the relationship between input and output using a line, called the regression line, that has a particular slope as well as a starting point, the intercept, which is an initial value added to each output and in this case sits around 35. Now, if we see the value 9 in the future as an input, we can assume the output would lie somewhere around 75. Note that this closely resembles our actual data where we see the (9.17, 77.89) pairing. Moving on, this corresponds on our regression line to an intercept of 35 + 9 scaled by the slope which might be around 40/9, or 4.5. Or in basic algebra y=mx+b: 75 = 4.5*9 +35. That’s all regression is! Basic algebra using scatter plots. That was really easy I think. Now keep in mind that we only have one input here. In a more conventional regression, we have many variables and each one has its own “slope,” or in other words, effect on output. We need to use more complex math to allow for the ability to measure the effect of every input. For this blog we will consider the single input case, though. It will allow us to have a discussion about how linear regression works as a concept and also give us a starting point to think about how we might change our approach, or really adjust our approach, as we move into data that is contextualized or described in 3 or more dimensions. Basic case: find effect of height on wingspan. Less basic case: find effect of height, weight, country, and birth year on life expectancy. Case 2 is far more complex but we will be able to address it by the end of the blog!

Assumptions

Not every data set is suited for linear regression; there are rules, or assumptions, that must be in place.

Assumption 1: Linearity. This one is probably one you already expected, just didn’t know you expected it. We can only use LINEAR regression if the relationship shown in the data is, you know, linear. If the trend in the scatter plot looks like it needs to be described using some higher degree polynomial or other type of non-linear function like a square root or logarithm than you probably can’t use linear regression. That being said, linear regression is only one method of supervised machine learning for predicting continuous outputs. There are many more options. Let’s use some visuals:

Linear Regression Analysis in SPSS Statistics - Procedure ...

Now, you may be wondering the following: this is pretty simple in the 2D case, but is it easy to test this assumption in higher dimensions? The answer is yes.

Assumption 2: Low Correlation Between Predictive Features. Our 2D case is an exception in a sense. We are only discussing the simple y=mx+b case here and the particular assumption listed above is more suited to multiple linear regression. Multiple linear regression is more like y= m1x1+m2x2+…+b. Basically, it has multiple independent variables. Say you are trying to predict how many points a game a player might score on any given night in the NBA and your features include things like height, weight, position, all-star games made, and some stats about how their vertical leap or running speed. Now, let’s say you also have the features that say a player’s age and what year they were drafted. Age and draft year are inherently correlated. We would probably not want to use both draft year and age. We know what this idea of reducing correlation means by using that example, but why is it important to reduce correlation? Well, one topic to understand is coefficients. Coefficients are basically the conclusion of a regression. They tell us how important each feature is and what its impact is on output. In the y=mx+b equation, m is the coefficient of x, the independent variable, and basically tells us how the dependent variable responds to each x value. So if you have an m value of 2 it means that the output variable increases by twice the value of the input variable. Say you are trying to predict NBA salary based on points per game. Well, let’s use two data points. Stephen Curry makes about $1.5M per point averaged and LeBron James makes about $1.4M per point averaged. Now, these players are outliers, but we get a basic idea that star players make like $1.45M per point averaged. That’s the point of regression; finding causal relationship between input and output. We lose the ability to find the impact of unique features on output when there are highly correlated features as they often move together and represent being tied together in certain ways.

Assumption 3: Homoscedasticity. Basically, what homoscedasticity means is that there is no “trend” in your data. What do I mean by “trend?”. By this, I mean that if you take a look at all the error values in your data (say your first value is 86 and you predict 87 and the second prediction is 88 but the true value is 89, then your first two errors are valued at 1 and -1), whether positive or negative, and plot it around the line y=0 representing no error, then we would not see a pattern in the resulting scatter plot and we might assume that the points around that line (y=0) would look to be rather random and most importantly, have constant variance. This plot we just described, that has a baseline of y=0 and error terms around it is called a residual plot. Let me give you the visual you have been waiting for in terms of residual plots. Also note that we didn’t discuss heteroscedasticity – but it’s basically the opposite of homoscedasticity, I think that’s quite obvious.

Assumptions Of Linear Regression Algorithm | by Gomathi ...

Assumption 4: Normality. This means that distribution of the error of the points that fall above and below the line is normally distributed. Note that this refers to the distribution of the value of the error (also called residuals – the value of which is calculated by subtracting the true value from the estimated value at every single value in the scatter plot measured against the closest value in the regression line), not the distribution of the y values. Here is a basic normal distribution. Hopefully, the largest portion of the value of the residuals fall around a center point (not necessarily at the value zero, it’s just an indicator of zero standard deviations from the mean – that’s what the x-axis is) and the amount of smaller and larger residuals appear in smaller quantities.

Extreme values: What is an extreme value for normally distributed ...

This next graph shows where the residuals should fall to have normality present, with E(y) representing the expected value (Credit to Brandon Foltz from YouTube for this visual).

Both graphs work, but at different scales.

Fitting A Line

Ok, so now that we have our key assumptions in place, we can start searching for the line that best fits the data. The particular method I’d like to discuss here is called ordinary least squares, or OLS. OLS sums up the difference between every predicted point and every true value (once again, each of those values is called a “residual,” which represents error) and squares this difference, adds it to the sum of residuals, and divides that final sum over the total number of data points. We call this metric MSE; mean squared error. So it’s basically finding the average error and looking for the model with lowest average error. To do this, we optimize the slope and intercept for the regression line so that each point is as close as possible to the true value as judged by MSE. As you can see by the GIF below, we start with a simple assumptions and move quickly toward the best line but slow down as we get closer and closer. (Also notice that we almost always start with assumption of a slope of zero. This is basically testing the hypothesis that input has no effect on output. In higher dimension, we always start with the simple assumption that every feature in our model has no effect on output and move closer to its true value carefully. This idea relates to a concept called gradient descent which will be discussed in the next blog in this series).

Linear Regression: The Easier Way | by SAGAR SHARMA | Towards Data ...

Now, one word you may notice that I used in the paragraph above is “optimize.” In case, you don’t already see where I’m going with this, we are going to need calculus. The following equation represents error and the metric we want to minimize as discussed above.

Tutorial: Understanding Linear Regression and Regression Error Metrics

That E looking letter is the Greek letter Sigma which represents a sum. The plain y is the true value (one exists for every value of x), and the y with a ^ (called y-hat) on top represents the predicted value. We basically square these terms so that we can look at error in absolute value terms. I would add a subscript of a little “n” next to every y and y-hat value to indicate that there are like a lot of these observations. Now keep in mind, this is going to be somewhat annoying to derive, but once we know what our metrics are we can use the formulas going forward. To start, we are going to expand the equation for a regression line and write it in a more formal way:

So, now we can look at MSE as follows:

This is the equation we need to optimize. To do this we will take the derivative with respect to all of our two unknown constants and set those results equal to zero. I’m going to do this by hand and add some pictures as typing it would take a while.

Step 1: Write down what needs to be written down; the basic formula, a formula where I rename the variables, and the partial derivatives for each unknown (If you don’t know what a partial derivative is that’s okay, it just tells us the equation we need to set equal to zero, because at zero we have a minimum in the value we are investigating, which is error in this case. Both error for slope value and error for intercept value. Those funky swirls that with the letters F on top and A or B below represent those equations).

Conclusion: We have everything we need to go forward.

Step 2: Solve one equation. We have two variables, and in case you don’t know how this works, we will therefore need two equations. Let’s start with the simpler equation.

Conclusion: A, or our intercept term equals the average of y, as indicated by the bar, minus the slope scaled by the average of x (keep in mind this is an average due to the 1/n, or “1 over N”, term not included. Also remember that for the end of the next calculation).

Step 3: Solve the other equation, using substitution (apologies for the rotation).

Conclusion: After a lot of math we got our answer. You may notice I took an extra step at the end and added a little box around that extra step. The reason for this is because that equation (hopefully, at the very least, you have encountered the denominator before) in that box is equal to the covariance between x and y divided by the variance of x. Those equations are fairly simple but are nevertheless beyond the scope of this blog. Let’s review how we calculate slope.

That was annoying, but we have our two metrics! Keep in mind that this process can be extended with increased complexity to higher dimensions. However, for those problems, which will be discussed in part 3, we are just going to use python and all its associated magic.

Evaluating Your Model

Now that we know how to build a basic slope-intercept model, how can we evaluate whether or not it is effective? Keep in mind that magnitude of the data you model may change which means that looking at MSE and only MSE will not be enough. We need the MSE to know what to optimize for low error, but we are going to need a bit more than that to evaluate a regression. Let’s now discuss R-Squared. R-Squared is a 0-1 or 0%-100% scale of how much variance is captured by our model. That sounds a bit weird and that’s because it’s a rather technical definition. R-Squared really answers the following question: How good is your model? Well, 0% means your model is the worst thing since the New York Yankees were introduced. A score in the 70%-90% range is more desirable. (100%, which you are no doubt wondering why I didn’t pick, means you probably overfit on training data and made a bad model). This is all nice, but how do we calculate this metric?

Looking at R-Squared. In data science we create regression… | by ...

One minus the sum of each prediction’s deviation from the true value divided each true value’s deviation from the mean (with both the numerator and denominator squared to account for that absolute value issue discussed earlier). You can probably guess the SS-RES label alludes to the concept of residuals and the sum of squares from residuals; true values minus the predicted values squared. The bottom refers to total sum of squares; a metric for deviation from the mean. In other words, (one minus) the amount of error in our model versus the amount of total error. There is also metric you may have heard of called “Adjusted R-Squared.” The idea behind this is to penalize excessively complex models. We are looking at a simple case here with only one true input, so it doesn’t really apply. Just know it exists for other models. Keep in mind that R-Squared doesn’t always measure how effective you in particular were at creating a model. It could be that it’s just a hard model to construct or one that will never work well independent of who creates the model. (Now you may be wondering how to people can have a different regression model. It’s a simple question but I think it’s important. The real difference between two models can present themselves in many ways. A key one, for example, is how one decides to pre-process their data. One person may remove outliers to different degrees than others and that can make a huge difference. Nevertheless, even though models are not all created equally, some have a lower celling or higher floor than others for R-Squared values).

Interpreting Residual Plots to Improve Your Regression - Qualtrics ...

Conclusion

I think if there’s one point to take home from this blog, it’s that linear regression is a relatively easy concept to wrap your head around. It’s very encouraging that such a basic concept is also highly valued as a skill to have as linear regression can be used to model many real world scenarios and has so many applications (like modeling professional athlete salaries or forecasting sales). Linear regression is also incredibly powerful because it can measure the effect of multiple inputs and their isolated impact on a singular output.

Let’s review. In this blog, we started by introducing a scenario to motivate interest in linear regression, discussed when it would be appropriate to conduct linear regression, broke down a regression equation into its core components, derived a formula for those components, and introduced metrics to evaluate the effectiveness of our model.

From my perspective, this blog presented me with a great opportunity to brush up on my skills in linear regression. I conduct linear regression models quite often (and we’ll see how those work in part 3) but don’t always spend a lot of time thinking about the underlying math and concepts, so writing this blog was quite enjoyable. I hope you enjoyed reading part 1 of this blog and will stick around for the next segment in this series. The next concept (in part 2, that is) I will discuss is a lesser known concept (compared to linear regression) called gradient descent. Stay tuned!

Sources and Further Reading

(https://warwick.ac.uk/fac/soc/economics/staff/vetroeger/teaching/po906_week567.pdf)

(http://www.mit.edu/~6.s085/notes/lecture3.pdf)

(https://medium.com/next-gen-machine-learning/r-square-coefficient-of-determination-f4f3c23329d9)

(https://medium.com/analytics-vidhya/r-squared-vs-adjusted-r-squared-a3ebc565677b)

(https://medium.com/@rahul77349/what-is-multicollinearity-5419c81e003f)

(https://towardsdatascience.com/linear-regression-for-data-science-1923256aba07)

(https://towardsdatascience.com/assumptions-of-linear-regression-algorithm-ed9ea32224e1)

Creative Ways to Say Thanks to Your Volunteers: Associations Now

Machine Learning Metrics and Confusion Matrices

Posted on August 2, 2020 by josephcohen94

Understanding the Elements and Metrics Derived from Confusion Matrices when Evaluating Model Performance in Machine Learning Classification

It Hurt Itself in Its Confusion! | Know Your Meme

Introduction

Thanks for visiting my blog.

I hope my readers get the joke displayed above. If they don’t and they’re also millennials, they missed out on some great childhood fun.

What are confusion matrices? Why do they matter? Well… a confusion matrix, in a relatively simple case, shows the distribution of predictions compared to real values in a machine learning classification model. Classification can theoretically have many target classes, but for this blog we are going to keep it simple and discuss prediction of a binary variable. In today’s blog, I’m going to explain the whole concept and how to understand confusion matrices on sight as well as the metrics you can pick up by looking at them.

Plan

Provide Visual
Accuracy
Recall
Precision
F-1
AUC-ROC Curve

Quick note: there are more metrics that derive from confusion matrices beyond what’s listed above. However, these are the most important and relevant metrics generally discussed.

Visualization

I have three visuals. The first one displays the actual logic behind confusion matrices while the second displays an example and the third displays a heat-map. Often, using a heat-map can be easier to decode and also easier to share with others. I’d like to also note that confusion matrix layouts can change. I would not get caught up on one particular format and just understand that rows correspond to predicted values columns correspond to actual values. The way the numbers within each of those are arranged is variable.

Basic explanation.

Understanding Confusion Matrix. When we get the data, after data ...

Now you will always have numbers in those quadrants and generally hope that the top left and bottom right have the highest values.

Confusion Matrix in Machine Learning - GeeksforGeeks

Heat-map.

As we can see above, knowing that red corresponds to higher values quickly gives us the reflection that our model worked well. In “error” locations, we have a strong blue color, while in “correct” areas we see a lot of red.

Before I get into the metrics, I need to quickly explain what TP, FP, TN, and FN mean. This won’t take long. TP is a true positive, like someone correctly being predicted to have a disease. TN is true negative, like someone correctly predicted to not have a disease. FN is a false negative, like some who was predicted to not have a disease but actually does. FP is a false positive, like some predicted to have a disease but actually doesn’t. This is a preview of some metrics to be discussed, but for certain models the importance of FN, FP, TN, and TP is variable and some may matter more than others.

Quick note: When I think of the words “accuracy” and “precision,” the first thing that comes to mind is what I learned back in Probability Theory; accuracy means unbiasedness and precision means minimal variance. I’ll talk about bias and variance in a later blog. For this blog, I’m not going to place too much focus on those particular definitions.

Accuracy

Accuracy is probably the most basic and simple idea. Accuracy is determined by summing true positive and true negative results over both the true positive and true negative predictions but also false positive and false negative predictions. In other words, of every single prediction you made, how many of them were right. So this means we want to know that if it was a negative how many times did you predict correctly and vice-versa for a positive. That being the case, when does accuracy become the most important metric to your model and when does accuracy fall short of being a strong or important metric? Let’s start with the cases where accuracy falls short. If you have a large class imbalance such as 10 billion rows in class 0 and 1 row in class 1, than you don’t necessarily have a strong model if it accurately predicts most of the majority class and predicts the minority class accurately the one time it occurs (or doesn’t predict the minority class correctly for that matter). Accuracy works well and tells a good story with more balanced data. However, as discussed above, it can lose meaning with a target class imbalance.

Here is a heat map of a high accuracy model.

Recall

Recall can most easily be described as true positives divided by true positives and false negatives. This corresponds to the number of positives correctly identified when in fact the case was positive. A false negative means an unidentified positive. False positives and true negatives are not meant to be positives (in a perfect model) so are not included. So if you are trying to identify if someone has a disease or not, having high recall would be good for you model since it means that when the disease is present, you identify it well. You could still have low accuracy or precision in this model if you don’t predict the non-disease class well. In other words if you predict every row as having the disease than your recall will be high since you will have correctly predicted every occurrence where the disease was actually present. Unfortunately, however, the impact of having a correct prediction will be diminished and mean a whole lot less. That leads us to precision.

Here is a heat map of a high recall model.

Precision

Precision can most easily be described as true positives divided by true positives and false positives. Unlike recall, which is a measure of actual positives discovered from the pool of all positives, precision is a measure of actual positives from predicted positives. So false negatives and true negatives don’t matter as they were not predicted to have been positive in the first place. A great way to think about precision is how meaningful a positive prediction is given the context of your model. Off the top of my head, I would assume that in a business where you owe some sort of service or compensation based on a predicted positive, having high precision would be important as you would not want to waste resources. I recently worked on an email spam detector. That is another example where high precision is ideal.

Here is a confusion matrix of a high precision model.

F-1 Score

The F-1 score is the harmonic mean of the precision and recall score which means its maximum value is the arithmetic mean of the two. (For more info on what a harmonic mean actually is – here is a Wikipedia page you may find helpful: https://en.wikipedia.org/wiki/Harmonic_mean). As you may have gathered or assumed from what’s written above, the F-1 score matters more in situations where accuracy may fall short.

Receiver Operating Curve (ROC) Curve

The basic description of this curve is that it measures how an increase in false positives to a model would correspond to increasing true positives which can evaluate your models ability to distinguish between classes. The horizontal axis values extend from 0% to 100% (or 0 to 1). The larger the area covered using the curve, the better your model is. You may be confused due to the lack of a visual. Let me show you what I mean:

How to Use ROC Curves and Precision-Recall Curves for ...

Above, the “No Skill” label means that you’ll get 50% of classifications right at random (don’t get too caught up on that point). The high increase early in the x values on the corresponding vertical axis are a good sign that as more information is introduced into your model, than its true positive rate climbs quickly. It maxes out around 30% and then begins a moderate plateau. This is a good sign and shows a lot of area covered by this orange curve. The more area covered, the better.

Conclusion

Confusion matrices are often a key part of machine learning models and can help tell and important story about the effectiveness of your model. Since there are varying ways data can present itself, it is important to have different metrics that derive from these matrices to measure success for each situation. Conveniently, you can view confusion matrices with relative ease using heat maps.

Sources and Further Reading

(https://towardsdatascience.com/metrics-to-evaluate-your-machine-learning-algorithm-f10ba6e38234)

(https://towardsdatascience.com/is-accuracy-everything-96da9afd540d)

(https://towardsdatascience.com/beyond-accuracy-precision-and-recall-3da06bea9f6c)

(https://towardsdatascience.com/understanding-auc-roc-curve-68b2303cc9c5)

Thank You Hand Drawn Lettering On Optical Illusion Background ...